
����Ŀ��ij�ؽ�����Ϊ�˷ḻ����ѧ���Ĵ�μ���Ҫ���ѧУ��չ��ʽ�����������������ij��ѧ����ѧ���������Ȥ�����������⣬��������˱�Уij���ѧ���������ݵ��������Ƴ����µIJ�����������ͳ��ͼ������ͳ��ͼ��
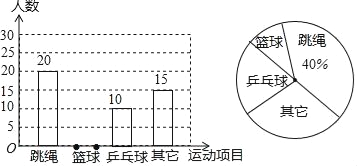
��1������ε����У�ϲ��������Ŀ��ͬѧ���� ���ˣ�������ͳ��ͼ�У���ƹ�������İٷֱ�Ϊ�� ��%�����ѧУ��800��ѧ��������ȫУѧ�������� ����ϲ��������Ŀ��
��2���뽫����ͳ��ͼ����������
��3���ڱ������ѧ���У�ϲ���������2��Ůͬѧ������Ϊ��ͬѧ����Ҫ���������ȡ2��ͬѧ�����༶�μ�У����ӣ���ֱ��д������ȡ��2��ͬѧǡ����1��Ůͬѧ��1����ͬѧ�ĸ��ʣ�
���𰸡���1��5��20��80����2��ͼ����������3��![]() .
.
�������������������1������������������������ռ�İٷֱȼ����������������������������ֱ��ȥϲ��������Ŀ�������ɵõ�ϲ��������Ŀ���������ټ����ϲ��ƹ������Ŀ�İٷֱȣ�Ȼ����800����������ϲ��������Ŀ�İٷֱȿɹ���ȫУѧ����ϲ��������Ŀ��������
��2�����ݣ�1������õ����ݿɲ�������ͳ��ͼ��
��3������״ͼչʾ����20�ֵȿ��ܵĽ���������ҳ�����ȡ��2��ͬѧǡ����1��Ůͬѧ��1����ͬѧ�Ľ������Ȼ����ݸ��ʹ�ʽ���.
�����������1�������������Ϊ20��40%=50���ˣ���
����ϲ��������Ŀ��ͬѧ������=50��20��10��15=5���ˣ���
��ƹ�������İٷֱ�=![]() =20%��
=20%��
��Ϊ800��![]() =80��
=80��
���Թ���ȫУѧ������80��ϲ��������Ŀ��
�ʴ�Ϊ5��20��80��
��2����ͼ��
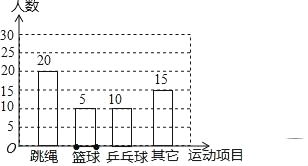
��3������״ͼΪ��

����20�ֵȿ��ܵĽ��������������ȡ��2��ͬѧǡ����1��Ůͬѧ��1����ͬѧ�Ľ����Ϊ12��
��������ȡ��2��ͬѧǡ����1��Ůͬѧ��1����ͬѧ�ĸ���=![]() =
=![]() ��
��


 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
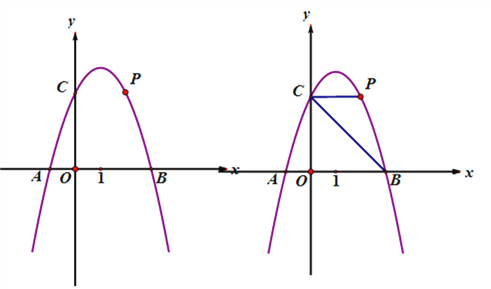
����Ŀ����ͼ��������![]() ��X���ڵ�A��B��A��B�ң�����Y���ڵ�C��
��X���ڵ�A��B��A��B�ң�����Y���ڵ�C�� ![]()
=6����PΪ��һ�������������ϵ�һ��.
��1���������ߵĽ���ʽ��
��2������PCB=45�㣬���P�����ꣻ
��3����QΪ������������������һ�㣬��Q�ĺ�����ȵ�P�ĺ������1������PC��
AQ����PC=![]() AQʱ�����P�������Լ���PCQ�����.
AQʱ�����P�������Լ���PCQ�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�У��Ե�PΪԲ�ĵ�Բ����x�ύ��A��B���㣬��֪P��4��2����A��2��0�������B��������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ(1)���ı���ABCD�У�AB��CD����ADC=90����P��A���������ÿ��1����λ���ȵ��ٶȣ���A��B��C��D��˳���ڱ��������˶�����P����˶�ʱ��Ϊt�룬��PAD�����ΪS��S����t�ĺ���ͼ����ͼ(2)��ʾ����P�˶���BC�е�ʱ����PAD�����Ϊ( )
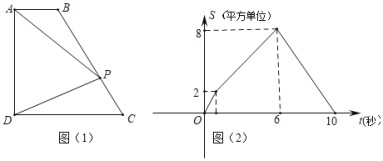
A. 4B. 5C. 6D. 7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��ֱ��Ϊ10cm�IJ������һ��Բ�ε�ţƤֽֽñ����һ����������ߣ������̵��������ͼ��ʾ��Բ��ĸ��AB���O�����ڵ�B�������̵Ķ���A������L����������18cm.����Բ��ֽñ����ȫͿ����ɫ����Ϳɫ���ֵ����Ϊ_____cm2.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����7��7�����У�ÿ��С�����εı߳���Ϊ1��
(1)�����ʵ���ƽ��ֱ������ϵ������A(1��3)��C(2��1)�����B������Ϊ______��
(2)��ABC�����Ϊ______��
(3)�жϡ�ABC����״����˵�����ɣ�
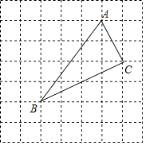
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ��ƽ̨Զ����һ��������С����ƽ̨�ײ��ĵ�C����ù�������B������Ϊ60������ƽ̨�ϵĵ�E����ù�������������Ϊ30������֪ƽ̨���ݽ���Ϊ����DCFE��DE=2�ף�DC=20�ף������AB�ĸߣ�����������ţ�
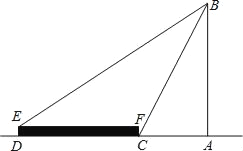
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ij����Ʒ�ĸ����븶����֮��Ĺ�ϵ
��1������ͼ��������б���
������Ʒ���������� | 2 | 4 | 6 | 7 |
��������Ԫ�� | �� �� | �� �� | �� �� | �� �� |
��2����д����ʾ������y��Ԫ���빺��������Ʒ�ĸ���x������֮��Ĺ�ϵʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����11����ۣ���ͼ��ʾ��������OEFG��������ABCD��λ��ͼ�Σ���F������
Ϊ(��1��1)����C������Ϊ(��4��2)����������������λ�����ĵ������� _ �� ��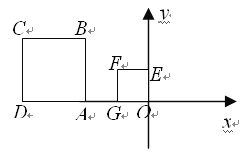
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com