
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D,AB,DC的延长线交于点E.
(1)求证:AC平分∠DAB;
(2)若BE=3,CE=3![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

【答案】(1)证明见解析;(2)![]()
【解析】
(1)连接OC,如图,利用切线的性质得CO⊥CD,则AD∥CO,所以∠DAC=∠ACO,加上∠ACO=∠CAO,从而得到∠DAC=∠CAO;
(2)设⊙O半径为r,利用勾股定理得到r2+27=(r+3)2,解得r=3,再利用锐角三角函数的定义计算出∠COE=60°,然后根据扇形的面积公式,利用S阴影=S△COE﹣S扇形COB进行计算即可.
解:(1)连接OC,如图,
∵CD与⊙O相切于点E,
∴CO⊥CD,
∵AD⊥CD,
∴AD∥CO,
∴∠DAC=∠ACO,
∵OA=OC,
∴∠ACO=∠CAO,
∴∠DAC=∠CAO,
即AC平分∠DAB;
(2)设⊙O半径为r,
在Rt△OEC中,∵OE2+EC2=OC2,
∴r2+27=(r+3)2,解得r=3,
∴OC=3,OE=6,
∴cos∠COE=![]() ,
,
∴∠COE=60°,
∴S阴影=S△COE﹣S扇形COB=![]() 33
33![]() ﹣
﹣![]() .
.


科目:初中数学 来源: 题型:
【题目】用一条直线截三角形的两边,若所截得的四边形对角互补,则称该直线为三角形第三条边上的逆平行线.如图1,DE为△ABC的截线,截得四边形BCED,若∠BDE+∠C=180°,则称DE为△ABC边BC的逆平行线.如图2,已知△ABC中,AB=AC,过边AB上的点D作DE∥BC交AC于点E,过点E作边AB的逆平行线EF,交边BC于点F.
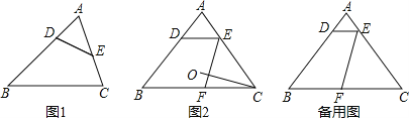
(1)求证:DE是边BC的逆平行线.
(2)点O是△ABC的外心,连接CO.求证:CO⊥FE.
(3)已知AB=5,BC=6,过点F作边AC的逆平行线FG,交边AB于点G.
①试探索AD为何值时,四边形AGFE的面积最大,并求出最大值;
②在①的条件下,比较AD+BG______AB大小关系.(“<、>或=”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,过点(﹣4,0),(0,﹣2).
(1)求抛物线的解析式和顶点坐标;
(2)当﹣4<x<4时,求y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节前夕举行了南通濠河国际龙舟邀请赛,在500米直道竞速赛道上,甲、乙两队所划行的路程y(单位:米)与时间t(单位:分)之间的函数关系式如图所示,根据图中提供的信息,有下列说法:①甲队比乙队提前0.5分到达终点②当划行1分钟时,甲队比乙队落后50米③当划行![]() 分钟时,甲队追上乙队④当甲队追上乙队时,两队划行的路程都是300米其中错误的是( )
分钟时,甲队追上乙队④当甲队追上乙队时,两队划行的路程都是300米其中错误的是( )
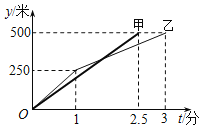
A. ①B. ②C. ③D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】居民区内的“广场舞”引起媒体关注,小王想要了解本小区居民对“广场舞”的看法,于是进行了-次抽样调查,把居民对“广场舞”的看法分为四类:
A.非常赞同; B.赞同但要有时间限制; C.无所谓; D.不赞同.
并将调查结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
(1)①本次被抽查的居民人数是________人;将条形统计图补充完整
②图l中∠α的度数是________度;该小区有3000名居民,请估计对“广场舞”表示赞同(包括A类和B类)的大约有________人.
(2)小王想从甲,乙,丙,丁四位居民中随机选取两位了解具体情况,请用列表或画树状图的方法求出恰好同时选中甲和乙两位居民的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD和菱形ECGF的边长分别为2和3,点D在CE上,且∠A=120°,B,C,G三点在同一直线上,则BD与CF的位置关系是_____;△BDF的面积是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com