Question

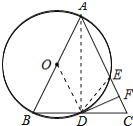
【题目】如图，已知△ABC，以AB为直径的⊙O交AC于点E，交BC于点D，且BD=CD，DF⊥AC于点F.给出以下四个结论：

①DF是⊙O的切线；②CF=EF；③=；④∠A=2∠FDC.

其中正确结论的序号是 .

Answer 1

【答案】①②④

【解析】

试题分析：由BD=DC，OA=OB，推出OD是△ABC的中位线，OD∥AC，由DF⊥AC得出得DF⊥OD，即DF是⊙O的切线，然后证出△ABC是等腰三角形，得出∠B=∠C，再推出△CDE为等腰三角形，从而推出∠A=2∠FDC，CF=EF.最后由假设推出≠；③不正确；即可得出结果.

解：连接OD、DE、AD，如图所示：

∵AB是⊙O的直径，

∴OA=OB，

∵DB=DC，

∴OD是△ABC的中位线，

∴OD∥AC，

∵DF⊥AC，

∴DF⊥OD.

∴DF是⊙O的切线，①正确；

∵DF是⊙O的切线，

∴∠CED=∠B，

∵AB是⊙O的直径，

∴∠ADB=90°，

即AD⊥BC，

∵BD=CD，

∴AB=AC，

∴∠B=∠C，

∴∠CED=∠C，

∴DC=DE，

又∵DF⊥AC，

∴CF=EF，②正确；

当∠EAD=∠EDA时，，

此时△ABC为等边三角形，

当△ABC不是等边三角形时，

∠EAD≠∠EDA，

则≠，

∴=不正确；

∵DF⊥AC，AD⊥BC，

∴∠FDC+∠C=∠CAD+∠C=90°，

∴∠FDC=∠CAD，

又AB=AC，

∴∠BAD=∠CAD，

∴∠A=2∠CAD=2∠FDC，④正确；

故答案为：①②④.