
【题目】如图,在△ABC中,AB=AC,点D在边BC上,连接AD .
(1)试利用尺规作图,求作:线段AE,使得AE是线段AD绕点A沿逆时针方向旋转得到的,且![]() (保留作图痕迹,不写作法于证明过程);
(保留作图痕迹,不写作法于证明过程);
(2)连接DE交AC于F,若![]() ,求
,求![]() 的度数.
的度数.

【答案】(1)答案见解析;(2)65°
【解析】
(1)做∠MAC=∠DAB,然后以A为圆心,AD为半径画弧,交AM于点E,线段AE即为所求;
(2)连接CE,由题意证明△ABD≌△ACE,然后利用等腰三角形和全等三角形的性质,分别表示出∠BAC,∠ACE与∠B的关系,从而列方程求解.
解:(1)如图所示,即为所求
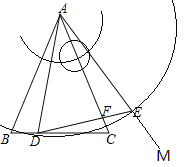
(2)连接CE
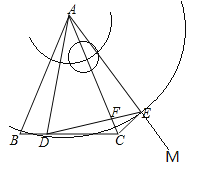
又题意可知“AB=AC,![]() ,AD=AE”
,AD=AE”
∴△ABD≌△ACE
∴∠B=∠ACE
∵![]()
∴∠BAC+∠CAE+∠AEC=165°
∵AB=AC
∴设∠B=x°,则∠BAC=(180-2x)°,∠ACE=x°
∴180-2x+180-x=165
解得:x=65
∴∠B的度数是65°


科目:初中数学 来源: 题型:
【题目】已知:直线![]() ,点
,点![]() ,
,![]() 分别是直线
分别是直线![]() ,
,![]() 上任意两点,在直线
上任意两点,在直线![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() ,在直线
,在直线![]() 上任取一点
上任取一点![]() ,作
,作![]() ,
,![]() 交直线
交直线![]() 于点
于点![]() .
.
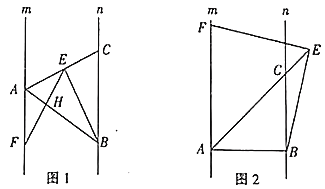
(1)如图1,若点![]() 是线段
是线段![]() 上任意一点,
上任意一点,![]() 交
交![]() 于
于![]() ,求证:
,求证:![]() ;
;
(2)如图2,点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() 与
与![]() 互为补角,若
互为补角,若![]() ,请判断线段
,请判断线段![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若 x 满足 (9x)(x4)=4, 求 (4x)2+(x9)2 的值.
设 9x=a,x4=b, 则 (9x)(x4)=ab=4,a+b=(9x)+(x4)=5 ,
∴(9x)2+(x4)2=a2+b2=(a+b)22ab=522×4=13
请仿照上面的方法求解下面问题:
(1)若 x 满足 (5x)(x2)=2, 求 (5x)2+(x2)2 的值
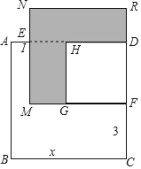
(2)已知正方形 ABCD 的边长为 x , E , F 分别是 AD 、 DC 上的点,且 AE=1 , CF=3 ,长方形 EMFD 的面积是 48 ,分别以 MF 、 DF 作正方形,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
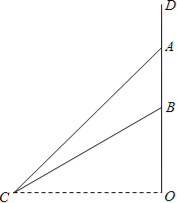
【题目】如图,水渠边有一棵大木瓜树,树干DO(不计粗细)上有两个木瓜A、B(不计大小),树干垂直于地面,量得AB=2米,在水渠的对面与O处于同一水平面的C处测得木瓜A的仰角为45°、木瓜B的仰角为30°.求C处到树干DO的距离CO.(结果精确到1米)(参考数据:![]() ,
,
![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c.
(Ⅰ)若抛物线的顶点为A(﹣2,﹣4),抛物线经过点B(﹣4,0)
①求该抛物线的解析式;
②连接AB,把AB所在直线沿y轴向上平移,使它经过原点O,得到直线l,点P是直线l上一动点.
设以点A,B,O,P为顶点的四边形的面积为S,点P的横坐标为x,当4+6![]() ≤S≤6+8
≤S≤6+8![]() 时,求x的取值范围;
时,求x的取值范围;
(Ⅱ)若a>0,c>1,当x=c时,y=0,当0<x<c时,y>0,试比较ac与l的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郑州市农业路高架桥二层的开通,较大程度缓解了市内交通的压力,最初设计南阳路口上桥匝道时,其坡角为15°,后来从安全角度考虑将匝道坡角改为5°(见示意图),如果高架桥高CD=6米,匝道BD和AD每米造价均为4 000元,那么设计优化后修建匝道AD的投资将增加多少元?(参考数据:sin5°≈0.08,sin15°≈0.25,tan5°≈0.09,tan15°≈0.27,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组在“用频率估计概率”的试验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的试验最有可能的是( )
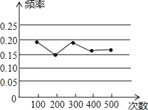
A. 在装有1个红球和2个白球(除颜色外完全相同)的不透明袋子里随机摸出一个球是“白球”
B. 从一副扑克牌中任意抽取一张,这张牌是“红色的”
C. 掷一枚质地均匀的硬币,落地时结果是“正面朝上”
D. 掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】班长小李对他所在班级(八年级![]() 班)全体同学的业余兴趣爱好进行了一次调查,据采集到的数据绘制了下面的统计图表,根据调查他想写一个调查报告交给学校,建议学校根据学生的个人兴趣爱好,适当的安排一些特长培养或合理安排学生在校期间的课余活动,请你根据图中提供的信息,帮助小李完成信息采集.
班)全体同学的业余兴趣爱好进行了一次调查,据采集到的数据绘制了下面的统计图表,根据调查他想写一个调查报告交给学校,建议学校根据学生的个人兴趣爱好,适当的安排一些特长培养或合理安排学生在校期间的课余活动,请你根据图中提供的信息,帮助小李完成信息采集.

(1)该班共有学生_____人;
(2)在图1中,请将条形统计图补充完整;
(3)在图2中,在扇形统计图中,“音乐”部分所对应的圆心角的度数_____度;
(4)求爱好“书画”的人数占该班学生数的百分数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:
①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1的实数).
其中正确结论的有( )

A. ①②③ B. ①③④ C. ③④⑤ D. ②③⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com