
����Ŀ��֣����ũҵ·���Ŷ���Ŀ�ͨ���ϴ�̶Ȼ��������ڽ�ͨ��ѹ��������������·�������ѵ�ʱ�����½�Ϊ15�㣬�����Ӱ�ȫ�Ƕȿ��ǽ��ѵ��½Ǹ�Ϊ5��(��ʾ��ͼ)��������Ÿ�CD��6�ף��ѵ�BD��ADÿ����۾�Ϊ4 000Ԫ����ô����Ż������ѵ�AD��Ͷ�ʽ����Ӷ���Ԫ��(�ο����ݣ�sin5���0.08��sin15���0.25��tan5���0.09��tan15���0.27�������������)

 ������������ϵ�д�
������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
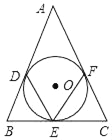
����Ŀ����ͼ����ABC�����߷ֱ��С�O��D��E��F��
��1������A��40�������DEF�Ķ�����
��2��AB��AC��13��BC��10�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �У�
��![]() ��������
��������![]() �Ƶ�
�Ƶ�![]() ��ת�õ�����
��ת�õ�����![]() ��ʹ��
��ʹ��![]() �Ķ�Ӧ��
�Ķ�Ӧ��![]() ����
����![]() �ϣ�
�ϣ�![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��ȡ��
��ȡ��![]() ��ʹ
��ʹ![]() ��
��
��1��֤��![]() ��
��
��2��![]() �Ķ�����
�Ķ�����
��3��֪![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
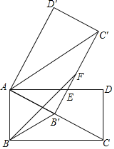
����Ŀ����ͼ1����֪������ABCD�ı�CD��������DEFG�ı�DE�ϣ�����AE��GC��
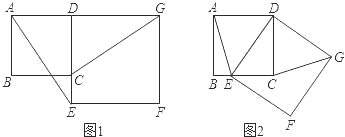
��1���Բ���AE��GC��������λ�ù�ϵ����֤����Ľ��ۣ�
��2����������DEFG�Ƶ�D��˳ʱ�뷽����ת��ʹ��E����BC���ϣ���ͼ2������AE��GC������Ϊ��1���еĽ����Ƿ�����������������֤����������������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC����D�ڱ�BC�ϣ�����AD .
��1�������ó߹���ͼ���������߶�AE��ʹ��AE���߶�AD�Ƶ�A����ʱ�뷽����ת�õ��ģ���![]() ��������ͼ�ۼ�����д������֤�����̣���
��������ͼ�ۼ�����д������֤�����̣���
��2������DE��AC��F����![]() ����
����![]() �Ķ���.
�Ķ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �У�
��![]() ����
����![]() ��ͬ������
��ͬ������![]() ����
����![]() ����
����![]() �����ı���
�����ı���![]() ��������ֵ�ǣ� ��
��������ֵ�ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=��x2+bx+c�ϲ��ֵ�ĺ�����x��������y�Ķ�Ӧֵ���±���ʾ��
x | �� | ��2 | ��1 | 0 | 1 | 2 | �� |
y | �� | 0 | 4 | 6 | 6 | 4 | �� |
���ϱ���֪������˵���У�������ǣ� ��
A. ��������x���һ����������Ϊ����2��0��
B. ��������y��Ľ�������Ϊ��0��6��
C. �����ߵĶԳ�����ֱ��x=0
D. �������ڶԳ�����ಿ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
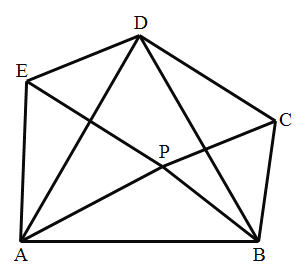
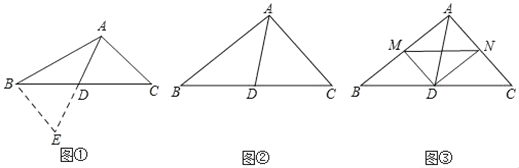
����Ŀ���������龳����ͼ�٣��ڡ�ABC�У���AB=10��AC=6����BC���ϵ�����AD��ȡֵ��Χ��
��1�������������ӳ�AD����EʹDE=AD��������BE����ACD���ŵ�D��ʱ����ת180���õ���EBD������AB��AC��2AD�����ڡ�ABE�У��������������ߵĹ�ϵ�����жϳ�����AD��ȡֵ��Χ���� ����
����˼������ʱ�����������������е����������������������Կ��ǹ����Ը��е�Ϊ�Գ����ĵ����ĶԳ�ͼ�Σ��ѷ�ɢ����֪����������֤�Ľ��ۼ��е�ͬ���������У��Ӷ�������⣮
��2��������Ӧ�ã���ͼ�ڣ���ABC�У���BAC=90����AD��BC���ϵ����ߣ��Բ����߶�AB��AC��AD֮���������ϵ����˵�����ɣ�
��3������չ���죩��ͼ�ۣ���ABC�У���BAC=90����D��BC���е㣬DM��DN��DM��AB�ڵ�M��DN��AC�ڵ�N������MN����BM=4��MN=5��AC=6ʱ����ֱ��д������AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�ADΪ��BAC��ƽ���ߣ�BM��AD,����ΪM,��AB=5,BM=2,AC=9,����ABC���C�Ĺ�ϵΪ�� ��

A.��ABC=2��CB.��ABC=![]() ��CC.
��CC.![]() ��ABC=��CD.��ABC=3��C
��ABC=��CD.��ABC=3��C
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com