
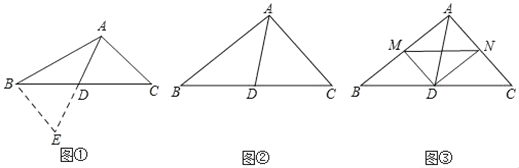
����Ŀ���������龳����ͼ�٣��ڡ�ABC�У���AB=10��AC=6����BC���ϵ�����AD��ȡֵ��Χ��
��1�������������ӳ�AD����EʹDE=AD��������BE����ACD���ŵ�D��ʱ����ת180���õ���EBD������AB��AC��2AD�����ڡ�ABE�У��������������ߵĹ�ϵ�����жϳ�����AD��ȡֵ��Χ���� ����
����˼������ʱ�����������������е����������������������Կ��ǹ����Ը��е�Ϊ�Գ����ĵ����ĶԳ�ͼ�Σ��ѷ�ɢ����֪����������֤�Ľ��ۼ��е�ͬ���������У��Ӷ�������⣮
��2��������Ӧ�ã���ͼ�ڣ���ABC�У���BAC=90����AD��BC���ϵ����ߣ��Բ����߶�AB��AC��AD֮���������ϵ����˵�����ɣ�
��3������չ���죩��ͼ�ۣ���ABC�У���BAC=90����D��BC���е㣬DM��DN��DM��AB�ڵ�M��DN��AC�ڵ�N������MN����BM=4��MN=5��AC=6ʱ����ֱ��д������AD�ij���
���𰸡���1��2��AD��8����2��AB2��AC2��4AD2�����ɼ���������3��AD��5��
��������
��1���ӳ�AD��E��ʹDE��AD����SAS֤����BDE�ա�CDA���ó�BE��AC��8������ABE�У��������ε����߹�ϵ���AE��ȡֵ��Χ�����ɵó�AD��ȡֵ��Χ��
��2���ӳ�AD��E��ʹDE��AD������BE����ͼ����ʾ���ɣ�1����֪��BDE�ա�CDA��Ȼ��ֻҪ֤����ABE��90�������ù��ɶ������ɵó����ۣ�
��3���ӳ�ND��E��ʹ��DN��DE������BE��EM������֤����BDE�ա�CDN�������ABD����DBE��90����Ȼ�����ù��ɶ����ɵ�BE��3�������õ�AN��NC���������ߺ�һ֤��DN��AC��ͬ���ɵ�DM��AB��Ȼ��֤���ı���AMDN�Ǿ��μ��ɽ������.
�⣺��1���ӳ�AD��E��ʹDE��AD������BE����ͼ����ʾ��
��AD��BC���ϵ����ߣ�
��BD��CD��
����BDE����CDA��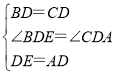 ��
��
���BDE�ա�CDA��SAS����
��BE��AC��6��
����ABE�У��������ε����߹�ϵ�ã�ABBE��AE��AB��BE��
��106��AE��10��6����4��AE��16��
��2��AD��8��
��2��AB2��AC2��4AD2��
���ɣ��ӳ�AD��E��ʹDE��AD������BE����ͼ����ʾ��
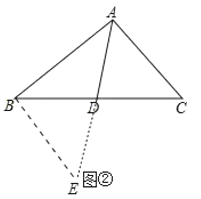
�ɣ�1����֪����BDE�ա�CDA��
��BE��AC����E����CAD��
�ߡ�BAC��90����
���E����BAE����BAE����CAD����BAC��90����
���ABE��90����
��AB2��BE2��AE2��
��AB2��AC2��4AD2��
��3����ͼ�ۣ��ӳ�ND��E��ʹ��DN��DE������BE��EM��
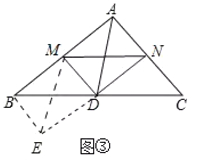
��BD��DC����BDE����CDN��DE��DN��
���BDE�ա�CDN��
��BE��CM����EBD����C��
�ߡ�ABC����C��90����
���ABD����DBE��90����
��MD��EN��DE��DN��
��ME��MN��5��
��Rt��BEM��BE��![]() ��3��
��3��
��CN��BE��3��
��AC��6��
��AN��NC��
�ߡ�BAC��90����BD��DC��
��AD��DC��BD��
��DN��AC��
��Rt��AMN��AM��![]() ��4��
��4��
��AM��BM��
��DA��DB��
��DM��
���AMD����AND����MAN��90����
���ı���AMDN�Ǿ��Σ�
��AD��MN��5��


 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
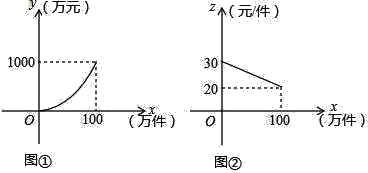
����Ŀ�������ڵ�����ʵʩ������ƶ�����ߵĺ����£�������չ�Ƽ���ƶ����������ũ���齨ũ����Ʒ���۹�˾��ijũ����Ʒ�������������100������ò�Ʒ����������y����Ԫ���������x�������֮��ĺ���ͼ���Ƕ���Ϊԭ��������ߵ�һ���֣���ͼ����ʾ�����ò�Ʒ�����۵���z��Ԫ/��������������x�������֮��ĺ���ͼ������ͼ����ʾ��һ���߶Σ��������IJ�Ʒ�����ڵ��������꣬�ﵽ����ƽ�⣬����ë����ΪW��Ԫ����ë����=���۶�������ã�
��1����ֱ��д��y��x�Լ�z��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2����W��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��������������������ʱ������ë����������ë�����Ƕ��٣�
��3���������ʽ��Ӱ�죬����Ͷ�������ķ��ò��ᳬ��360��Ԫ���������ɻ�ö�����Ԫ��ë����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��֣����ũҵ·���Ŷ���Ŀ�ͨ���ϴ�̶Ȼ��������ڽ�ͨ��ѹ��������������·�������ѵ�ʱ�����½�Ϊ15�㣬�����Ӱ�ȫ�Ƕȿ��ǽ��ѵ��½Ǹ�Ϊ5��(��ʾ��ͼ)��������Ÿ�CD��6�ף��ѵ�BD��ADÿ����۾�Ϊ4 000Ԫ����ô����Ż������ѵ�AD��Ͷ�ʽ����Ӷ���Ԫ��(�ο����ݣ�sin5���0.08��sin15���0.25��tan5���0.09��tan15���0.27�������������)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����Ƴ���һ����ͼ��ʾ��ת�̣�ȡ��Ϊ�����Ĵ�ת��������Ϸ�涨������������ת��ת�̣�ת��ֹͣ����ָ��ָ����ĸ��A�������շ�2Ԫ����ָ��ָ����ĸ��B��������3Ԫ����ָ��ָ����ĸ��C��������1Ԫ��һ�죬ǰ��Ѱ���ĵ���ת��ת��80�Σ�����Ϊ��������ӯ���Ŀ����Դ��ǿ���Ŀ����Դ�Ϊʲô��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���С��������ڰ༶�����꼶![]() �ࣩȫ��ͬѧ��ҵ����Ȥ���ý�����һ�ε��飬�ݲɼ��������ݻ����������ͳ��ͼ�������ݵ�������дһ�����鱨�潻��ѧУ������ѧУ����ѧ���ĸ�����Ȥ���ã��ʵ��İ���һЩ�س��������������ѧ����У�ڼ�Ŀ������������ͼ���ṩ����Ϣ������С�������Ϣ�ɼ�.
�ࣩȫ��ͬѧ��ҵ����Ȥ���ý�����һ�ε��飬�ݲɼ��������ݻ����������ͳ��ͼ�������ݵ�������дһ�����鱨�潻��ѧУ������ѧУ����ѧ���ĸ�����Ȥ���ã��ʵ��İ���һЩ�س��������������ѧ����У�ڼ�Ŀ������������ͼ���ṩ����Ϣ������С�������Ϣ�ɼ�.

��1���ð��ѧ��_____�ˣ�
��2����ͼ1�У��뽫����ͳ��ͼ����������
��3����ͼ2�У�������ͳ��ͼ�У�����������������Ӧ��Բ�ĽǵĶ���_____�ȣ�
��4�������黭��������ռ�ð�ѧ�����İٷ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ѽ��̳���ij���·�ÿ���ijɱ�Ϊ![]() Ԫ����������Ա���鷢�֣�ÿ�¸��·���������
Ԫ����������Ա���鷢�֣�ÿ�¸��·���������![]() ����λ�����������۵���
����λ�����������۵���![]() ����λ��Ԫ/����֮�������ͼ���߶�
����λ��Ԫ/����֮�������ͼ���߶�![]() ��ʾ�Ĺ��ɣ�
��ʾ�Ĺ��ɣ�
��1����![]() ��
��![]() ֮��ĺ�����ϵʽ����д��
֮��ĺ�����ϵʽ����д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����ij�¸��̳����������·��������Ϊ![]() Ԫ������������·������۵���Ϊÿ������Ԫ��
Ԫ������������·������۵���Ϊÿ������Ԫ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��1����2��Ҫʹ��ABD����ACD�������������������һ���������ѡ���ǣ� ��

A.��ADB����ADCB.��B����CC.AB��ACD.DB��DC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
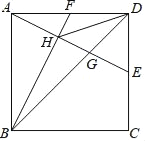
����Ŀ����֪��������ABCD�У�AB=4��EΪCD���е㣬FΪAD���е㣬AE��BD��G����BF��H������DH��
��1����֤��BG=2DG��
��2����AH��HG��GE��ֵ��
��3����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com