
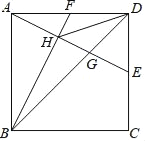
【题目】已知:正方形ABCD中,AB=4,E为CD边中点,F为AD边中点,AE交BD于G,交BF于H,连接DH.
(1)求证:BG=2DG;
(2)求AH:HG:GE的值;
(3)求![]() 的值.
的值.
【答案】(1)详见解析;(2)AH:HG:GE =6:4:5;(3)![]() .
.
【解析】
(1)利用平行线分线段成比例定理即可解决问题;
(2)分别求出AH、GH、GE即可解决问题;
(3)作DM⊥AE于M.分别求出DH、BH即可;
(1)证明:∵四边形ABCD是正方形,
∵AB∥CD,AB=CD,
∵E为CD边中点,
∴![]() ,
,
∴![]() ,
,
∴BG=2DG.
(2)解:∵AB∥CD,AB=CD,
∵E为CD边中点,
∴![]()
∴![]() ,
,
∴![]() ,
,
在Rt△ADE中,∵AD=4,DE=2,
∴AE=![]() ,
,
∴EG=![]() ,
,
同理可得BF=![]() ,
,
∵AB=AD,∠BAF=∠ADE,AF=DE,
∴△BAF≌△ADE,
∴∠ABF=∠DAE,
∵∠DAE+∠BAH=90°,
∴∠ABF+∠BAH=90°,
∴∠AHB=90°,
∴AE⊥BF,
∴![]() ,
,
∴AH=![]() ,
,
∴HG=![]() 2,
2,
∴AH:HG:GE=![]() =6:4:5.
=6:4:5.
(3)作DM⊥AE于M.
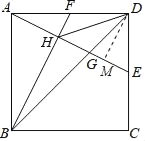
由(2)可知:DM=AH=![]() ,
,
在Rt△DME中,
∴EM=![]() =
=![]() ,
,
∴HM=AE-AH-EM=2![]() -
- ![]() -
-![]() =
=![]() ,
,
在Rt△DHM中,
∴DH=![]() =
=![]() ,
,
在Rt△AHB中,
∵BH=![]() =
=![]() ,
,
∴![]() =
=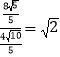 .
.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
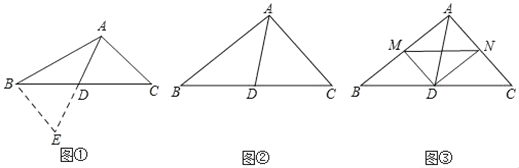
【题目】(问题情境)如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
(1)(问题解决)延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形三边的关系即可判断出中线AD的取值范围是 .
(反思感悟)解题时,条件中若出现“中点”、“中线”字样,可以考虑构造以该中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同个三角形中,从而解决问题.
(2)(尝试应用)如图②,△ABC中,∠BAC=90°,AD是BC边上的中线,试猜想线段AB,AC,AD之间的数量关系,并说明理由.
(3)(拓展延伸)如图③,△ABC中,∠BAC=90°,D是BC的中点,DM⊥DN,DM交AB于点M,DN交AC于点N,连接MN.当BM=4,MN=5,AC=6时,请直接写出中线AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD为∠BAC的平分线,BM⊥AD,垂足为M,且AB=5,BM=2,AC=9,则∠ABC与∠C的关系为( )

A.∠ABC=2∠CB.∠ABC=![]() ∠CC.
∠CC.![]() ∠ABC=∠CD.∠ABC=3∠C
∠ABC=∠CD.∠ABC=3∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校有2000名学生,为了解全校学生的上学方式,我校数学兴趣小组在全校随机抽取了150名学生进行抽样调查。整理样本数据,得到下列图表:


(1)若150名学生都在同一个年级抽取,这样的抽样是否合理?_______(填“是”或“否”);
(2)根据调查结果,估计全校2000名学生上学方式的情况:步行______人;骑车_____人;乘公共交通工具_______人; 乘私家车_____人;其它_______人,并绘制成条形统计图;

(3)数学兴趣小组结合调查获取的信息,向学校提出了一些建议。如:骑车上学的学生数约占全校的34%,建议学校合理安排自行车停车场地。请你结合上述统计的全过程,再提出一条合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFMN的一边MN在边BC上,顶点E、F分别在AB、AC上,其中BC=24cm,高AD=12cm.
(1)求证:△AEF∽△ABC:
(2)求正方形EFMN的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在AB边上,DE∥BC,与边AC交于点E,连结BE.记△ADE,△BCE的面积分别为S1,S2,( )
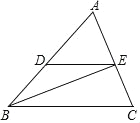
A. 若2AD>AB,则3S1>2S2 B. 若2AD>AB,则3S1<2S2
C. 若2AD<AB,则3S1>2S2 D. 若2AD<AB,则3S1<2S2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() ,
,![]() 与
与![]() 和
和![]() 分别相切于点
分别相切于点![]() 和点
和点![]() .点
.点![]() 和点
和点![]() 分别是
分别是![]() 和
和![]() 上的动点,
上的动点,![]() 沿
沿![]() 和
和![]() 平移.
平移.![]() 的半径为
的半径为![]() ,
,![]() .下列结论错误的是( )
.下列结论错误的是( )
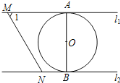
A. ![]() B.
B. ![]() 和
和![]() 的距离为
的距离为![]()
C. 若![]() ,则
,则![]() 与
与![]() 相切 D. 若
相切 D. 若![]() 与
与![]() 相切,则
相切,则![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
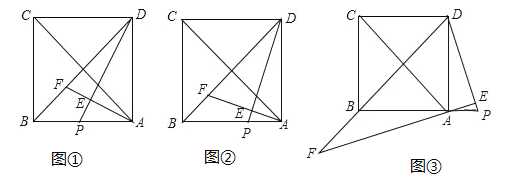
【题目】如图,在边长为6的正方形ABCD中,点P为AB上一动点,连接DB、DP,AE⊥DP于E.
(1)如图①,若P为AB的中点,则![]() = ;
= ;![]() = ;
= ;
(2)如图②,若![]() 时,证明:AC=4BF;
时,证明:AC=4BF;
(3)如图③,若P在BA的延长线上,当![]() = 时,
= 时,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com