
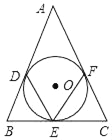
【题目】如图,△ABC的三边分别切⊙O于D,E,F.
(1)若∠A=40°,求∠DEF的度数;
(2)AB=AC=13,BC=10,求⊙O的半径.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,点E在边AD上,连接BE将△ABE沿BE翻折,得到△MBE,M点刚好在CD边上,若AD长为2,AB长为![]() ,则AE=_____.
,则AE=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线![]() ,点
,点![]() ,
,![]() 分别是直线
分别是直线![]() ,
,![]() 上任意两点,在直线
上任意两点,在直线![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() ,在直线
,在直线![]() 上任取一点
上任取一点![]() ,作
,作![]() ,
,![]() 交直线
交直线![]() 于点
于点![]() .
.
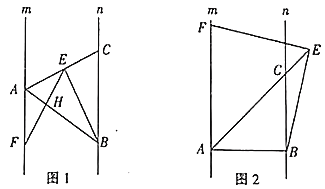
(1)如图1,若点![]() 是线段
是线段![]() 上任意一点,
上任意一点,![]() 交
交![]() 于
于![]() ,求证:
,求证:![]() ;
;
(2)如图2,点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() 与
与![]() 互为补角,若
互为补角,若![]() ,请判断线段
,请判断线段![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 在![]() .
.
(1)用尺规作图方法,按要求作图:
①作![]() 的高
的高![]() ;
;
②作![]() 的平分线
的平分线![]() ,分别交
,分别交![]() 于点
于点![]() ;
;
(要求:保留作图痕迹,不写作法和证明)
(2)求证:点![]() 在
在![]() 的垂直平分线.上; .
的垂直平分线.上; .
(3)在(1)所作的图中,探究线段AE与BF的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数学活动课上,小丽为了测量校园内旗杆AB的高度,站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.已知旗杆与教学楼的距离BD=9m,请你帮她求出旗杆的高度(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
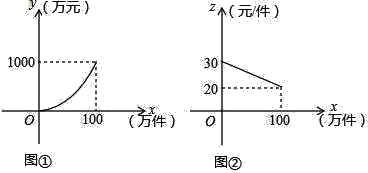
【题目】我市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点为原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为W万元.(毛利润=销售额﹣生产费用)
(1)请直接写出y与x以及z与x之间的函数关系式;(写出自变量x的取值范围)
(2)求W与x之间的函数关系式;(写出自变量x的取值范围);并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
(3)由于受资金的影响,今年投入生产的费用不会超过360万元,今年最多可获得多少万元的毛利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郑州市农业路高架桥二层的开通,较大程度缓解了市内交通的压力,最初设计南阳路口上桥匝道时,其坡角为15°,后来从安全角度考虑将匝道坡角改为5°(见示意图),如果高架桥高CD=6米,匝道BD和AD每米造价均为4 000元,那么设计优化后修建匝道AD的投资将增加多少元?(参考数据:sin5°≈0.08,sin15°≈0.25,tan5°≈0.09,tan15°≈0.27,结果保留整数)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com