
【题目】菱形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 上一个动点,
上一个动点,![]() ,连接
,连接![]() 并延长交
并延长交![]() 延长线于点
延长线于点![]() .
.
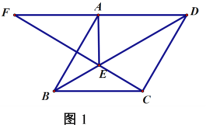
(1)如图1,求证:![]() ;
;
(2)当![]() 为直角三角形时,求
为直角三角形时,求![]() 的长;
的长;
(3)当![]() 为
为![]() 的中点,求
的中点,求![]() 的最小值.
的最小值.
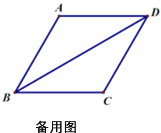
【答案】(1)详见解析;(2)当![]() 为直角三角形时,
为直角三角形时,![]() 的长是
的长是![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
(1)先根据菱形的性质证![]() ,再证
,再证![]() ,由全等的性质可得
,由全等的性质可得![]() ,进而得出结论;
,进而得出结论;
(2)分以下两种情况讨论:①![]() ,②
,②![]() ;
;
(3)过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,当
,当![]() 三点在同一直线上且
三点在同一直线上且![]() 时
时![]() 的值最小,即为
的值最小,即为![]() 的长.
的长.
解:(1)![]() 四边形
四边形![]() 是菱形,
是菱形,
![]() ,
,![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,
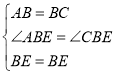
![]() ,
,
![]() ,
,
![]() .
.
(2)连接![]() 交
交![]() 于点
于点![]() ,
,

![]() 四边形
四边形![]() 是菱形,
是菱形,
![]() ,
,![]() .
.
又∠ABC=60°,∴△ABC为等边三角形,
∴![]() ,
,![]() .
.
∴![]()
![]() .
.
∴![]() .
.
![]() ,
,
![]() .
.
当![]() 时,有
时,有![]() ,
,
在![]() 中,
中,
![]() ,
,
![]() 设
设![]() ,
,![]() ,
,
![]() ,
,
![]() ,解得
,解得![]() .
.
![]() .
.
![]() .
.
当![]() 时,有
时,有![]() ,
,
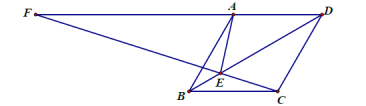
由![]() 知
知![]() ,
,
![]() 是等腰直角三角形.
是等腰直角三角形.
![]()
![]() .
.
综上:当![]() 为直角三角形时,
为直角三角形时,![]() 的长是
的长是![]() 或
或![]() .
.
(3)过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,
,
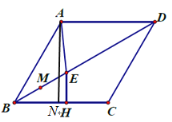
在![]() 中,
中,
![]()
![]()
又![]() 是
是![]() 的中点,
的中点,![]()
![]()
![]() .
.
当![]() 三点在同一直线上且
三点在同一直线上且![]() 时
时
![]() 的值最小,即为
的值最小,即为![]() 的长.
的长.
在![]() 中,
中,
![]() ,
,![]() ,
,
![]() ,
,
∴![]() .
.
![]() 的最小值是
的最小值是![]() .
.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点,若AE=2,当EF+CF取得最小值时,则∠BCF的度数为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.现把拱桥的截面图放在平面直角坐标系中,如图(2).


求(1)抛物线的解析式;
(2)两盏景观灯P1、P2之间的水平距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)
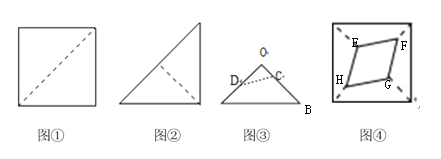
将一张正方形纸片按如图步骤①②,沿虚线对折2次,然后沿图③的虚线剪去一个角,展开铺平后得到图④,若图③中![]() ,
,![]() ,则四边形
,则四边形![]() 与原正方形纸面积比为( )
与原正方形纸面积比为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011内蒙古赤峰,7,3分)早晨,小张去公园晨练,下图是他离家的距离y(千
米)与时间t(分钟)的函数图象,根据图象信息,下列说法正确的是 ( )

A.小张去时所用的时间多于回家所用的时间B.小张在公园锻炼了20分钟
C.小张去时的速度大于回家的速度 D.小张去时走上坡路,回家时走下坡路
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两位老师同住一小区,该小区与学校相距![]() 米.甲从小区步行去学校,出发
米.甲从小区步行去学校,出发![]() 分钟后乙再出发,乙从小区先骑公共自行车,骑行若干米到达还车点后,立即步行走到学校.已知乙骑车的速度为
分钟后乙再出发,乙从小区先骑公共自行车,骑行若干米到达还车点后,立即步行走到学校.已知乙骑车的速度为![]() 米/分,甲步行的速度比乙步行的速度每分钟快
米/分,甲步行的速度比乙步行的速度每分钟快![]() 米.设甲步行的时间为
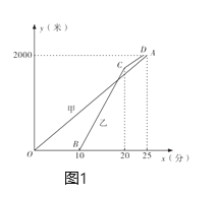
米.设甲步行的时间为![]() (分),图1中线段
(分),图1中线段![]() 与折线
与折线![]() 分别表示甲、乙离小区的路程
分别表示甲、乙离小区的路程![]() (米)与甲步行时间
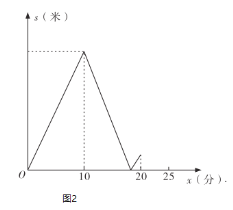
(米)与甲步行时间![]() (分)的函数关系的图象;图2表示甲、乙两人之间的距离
(分)的函数关系的图象;图2表示甲、乙两人之间的距离![]() (米)与甲步行时间
(米)与甲步行时间![]() (分)的函数关系的图象(不完整),根据图1和图2中所给的信息,解答下列问题:
(分)的函数关系的图象(不完整),根据图1和图2中所给的信息,解答下列问题:
(1)求甲步行的速度和乙出发时甲离开小区的路程;
(2)求直线![]() 的解析式;
的解析式;
(3)在图2中,画出当![]() 时,
时,![]() 关于
关于![]() 的函数的大致图象.
的函数的大致图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知正方形ABCD的边CD在正方形DEFG的边DE上,连接AE,GC.
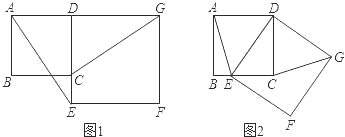
(1)试猜想AE与GC有怎样的位置关系,并证明你的结论;
(2)将正方形DEFG绕点D按顺时针方向旋转,使点E落在BC边上,如图2,连接AE和GC.你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com