
【题目】如图(1)是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.现把拱桥的截面图放在平面直角坐标系中,如图(2).


求(1)抛物线的解析式;
(2)两盏景观灯P1、P2之间的水平距离.
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】尺规作图:
已知:线段AB,BC,∠ABC=90°,求作:矩形ABCD.
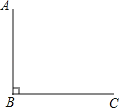
下面是小敏设计的尺规作图过程:
做法:①以点C为圆心,AB长为半径画弧;
②以点A为圆心,BC长为半径画弧;
③两弧在BC上方交于点D连接AD,CD,四边形ABCD即为所求
根据小敏设计的尺规作图过程,
(1)使用直尺和圆规补全图形;(保留作图痕迹)
(2)完成下面的证明
证明:∵AB= ,CB= ,
∴四边形ABCD为平行四边形( )
又∵∠ABC90°
∴平行四边形ABCD为矩形( )(填推理依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,点E在边AD上,连接BE将△ABE沿BE翻折,得到△MBE,M点刚好在CD边上,若AD长为2,AB长为![]() ,则AE=_____.
,则AE=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于点E,连接CE.
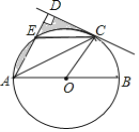
(1)判断CD与⊙O的位置关系,并证明你的结论;
(2)若E是弧AC的中点,⊙O的半径为2,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
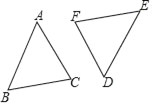
【题目】如图,△ABC和△DEF关于点O成中心对称.
(1)作出它们的对称中心O,并简要说明作法;
(2)若AB=6,AC=5,BC=4,求△DEF的周长;
(3)连接AF,CD,试判断四边形ACDF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
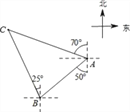
【题目】如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )
A. 10![]() 海里 B. 10
海里 B. 10![]() 海里 C. 10
海里 C. 10![]() 海里 D. 20
海里 D. 20![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
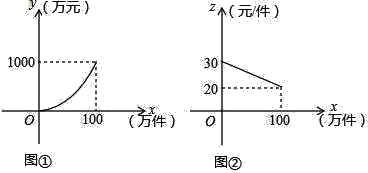
【题目】我市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点为原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为W万元.(毛利润=销售额﹣生产费用)
(1)请直接写出y与x以及z与x之间的函数关系式;(写出自变量x的取值范围)
(2)求W与x之间的函数关系式;(写出自变量x的取值范围);并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
(3)由于受资金的影响,今年投入生产的费用不会超过360万元,今年最多可获得多少万元的毛利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com