
【题目】如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于点E,连接CE.
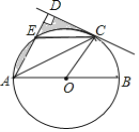
(1)判断CD与⊙O的位置关系,并证明你的结论;
(2)若E是弧AC的中点,⊙O的半径为2,求图中阴影部分的面积.
【答案】(1)CD与圆O相切,证明见解析;(2)![]() ;
;
【解析】
(1)只要证明OC∥AD即可解决问题.
(2)只要证明四边形AECO是菱形,∠DEC=∠DAO=60°,根据S阴影=S△DEC即可解决问题.
(1)CD与圆O相切,理由如下:
∵AC为∠DAB的平分线,
∴∠DAC=∠BAC,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠DAC=∠OCA,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥CD,
则CD与圆O相切;
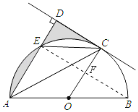
(2)连接EB,交OC于F,
∵AB为直径,
∴∠AEB=90°,
∴EB∥CD,
∵CD与⊙O相切,C为切点,
∴OC⊥CD,
∴OC∥AD,
∴∠EAC=∠ACO,
∵弧AE=弧EC,
∴AE=EC,
∴∠EAC=∠ECA,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠ECA=∠OAC,
∴EC∥OA,
∴四边形AECO是平行四边形,
∵OA=OC,
∴四边形AECO是菱形,
∴AE=EC=OA=OC=2,易知∠DEC=∠DAO=60°,
∴DE=![]() EC=1,DC=
EC=1,DC=![]() DE=
DE=![]()
∵点O为AB的中点,∴OF为ΔABE的中位线,
∴OF=![]() AE=1,即CF=DE=1,在RtΔOBF中,根据勾股定理得:EF=FB=DC=
AE=1,即CF=DE=1,在RtΔOBF中,根据勾股定理得:EF=FB=DC=![]() ,
,
则![]() .
.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】某文具店购进A,B两种钢笔,若购进A种钢笔2支,B种钢笔3支,共需90元;购进A种钢笔3支,B种钢笔5支,共需145元.
(1)求A、B两种钢笔每支各多少元?
(2)若该文具店要购进A,B两种钢笔共90支,总费用不超过1588元,并且A种钢笔的数量少于B种钢笔的数量,那么该文具店有哪几种购买方案?
(3)文具店以每支30元的价格销售B种钢笔,很快销售一空,于是,文具店决定在进价不变的基础上再购进一批B种钢笔,涨价卖出,经统计,B种钢笔售价为30元时,每月可卖68支;每涨价1元,每月将少卖4支,设文具店将新购进的B种钢笔每支涨价a元(a为正整数),销售这批钢笔每月获利W元,试求W与a之间的函数关系式,并且求出B种铅笔销售单价定为多少元时,每月获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点,若AE=2,当EF+CF取得最小值时,则∠BCF的度数为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,AB=2,AD和BE是圆O的两条切线,A,B为切点,过圆上一点C作⊙O的切线CF,分别交AD,BE于点M,N,连接AC,CB.若∠ABC=30°,则AM等于( )

A. 0.5 B. 1 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
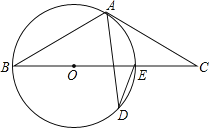
【题目】如图,BE是O的直径,点A和点D是⊙O上的两点,过点A作⊙O的切线交BE延长线于点.
(1)若∠ADE=25°,求∠C的度数;
(2)若AB=AC,CE=2,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.现把拱桥的截面图放在平面直角坐标系中,如图(2).


求(1)抛物线的解析式;
(2)两盏景观灯P1、P2之间的水平距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)
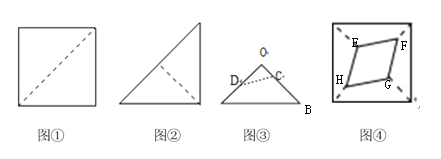
将一张正方形纸片按如图步骤①②,沿虚线对折2次,然后沿图③的虚线剪去一个角,展开铺平后得到图④,若图③中![]() ,
,![]() ,则四边形
,则四边形![]() 与原正方形纸面积比为( )
与原正方形纸面积比为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
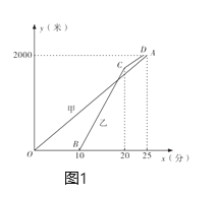
【题目】甲乙两位老师同住一小区,该小区与学校相距![]() 米.甲从小区步行去学校,出发
米.甲从小区步行去学校,出发![]() 分钟后乙再出发,乙从小区先骑公共自行车,骑行若干米到达还车点后,立即步行走到学校.已知乙骑车的速度为
分钟后乙再出发,乙从小区先骑公共自行车,骑行若干米到达还车点后,立即步行走到学校.已知乙骑车的速度为![]() 米/分,甲步行的速度比乙步行的速度每分钟快
米/分,甲步行的速度比乙步行的速度每分钟快![]() 米.设甲步行的时间为
米.设甲步行的时间为![]() (分),图1中线段
(分),图1中线段![]() 与折线
与折线![]() 分别表示甲、乙离小区的路程
分别表示甲、乙离小区的路程![]() (米)与甲步行时间
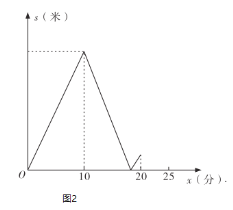
(米)与甲步行时间![]() (分)的函数关系的图象;图2表示甲、乙两人之间的距离
(分)的函数关系的图象;图2表示甲、乙两人之间的距离![]() (米)与甲步行时间
(米)与甲步行时间![]() (分)的函数关系的图象(不完整),根据图1和图2中所给的信息,解答下列问题:
(分)的函数关系的图象(不完整),根据图1和图2中所给的信息,解答下列问题:
(1)求甲步行的速度和乙出发时甲离开小区的路程;
(2)求直线![]() 的解析式;
的解析式;
(3)在图2中,画出当![]() 时,
时,![]() 关于
关于![]() 的函数的大致图象.
的函数的大致图象.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com