
【题目】如图,已知AB是⊙O的直径,AB=2,AD和BE是圆O的两条切线,A,B为切点,过圆上一点C作⊙O的切线CF,分别交AD,BE于点M,N,连接AC,CB.若∠ABC=30°,则AM等于( )

A. 0.5 B. 1 C. ![]() D.
D. ![]()
【答案】C
【解析】
连接OM,OC,由OB=OC,且∠ABC的度数求出∠BCO的度数,利用外角性质求出∠AOC度数,利用切线长定理得到MA=MC,利用HL得到三角形AOM与三角形COM全等,利用全等三角形对应角相等得到OM为角平分线,求出∠AOM为30°,在直角三角形AOM中,利用锐角三角函数定义即可求出AM的长.
连接OM,OC,
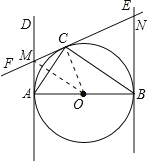
∵OB=OC,且∠ABC=30°,
∴∠BCO=∠ABC=30°,
∵∠AOC为△BOC的外角,
∴∠AOC=2∠ABC=60°,
∵MA,MC分别为圆O的切线,
∴MA=MC,且∠MAO=∠MCO=90°,
在Rt△AOM和Rt△COM中,
![]()
∴Rt△AOM≌Rt△COM(HL),
∴![]()
在Rt△AOM中,![]()
∴![]() 即
即![]()
解得:![]()
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
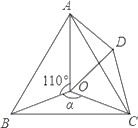
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆柱形杯子高9cm,底面周长18cm,在杯口点B处有一滴蜂蜜,此时蚂蚁在杯外底部与蜂蜜相对的点A处.
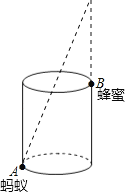
(1)求蚂蚁从A到B处杯壁爬行吃到蜂蜜的最短距离;
(2)若蚂蚁出发时发现有蜂蜜正以每秒钟1cm沿杯内壁下滑,蚂蚁出发后3秒钟吃到了蜂蜜,求蚂蚁的平均速度至少是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列五个命题:![]() 两个端点能够重合的弧是等弧;
两个端点能够重合的弧是等弧;![]() 圆的任意一条弧必定把圆分成劣弧和优弧两部分
圆的任意一条弧必定把圆分成劣弧和优弧两部分![]() 经过平面上任意三点可作一个圆;
经过平面上任意三点可作一个圆;![]() 任意一个圆有且只有一个内接三角形
任意一个圆有且只有一个内接三角形![]() 三角形的外心到各顶点距离相等.其中真命题有( )
三角形的外心到各顶点距离相等.其中真命题有( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,点E在边AD上,连接BE将△ABE沿BE翻折,得到△MBE,M点刚好在CD边上,若AD长为2,AB长为![]() ,则AE=_____.
,则AE=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮和妈妈从家出发到长嘉汇观看国庆灯光秀,妈妈先出发,2分钟后小亮沿同一路线出发去追妈妈,当小亮追上妈妈时发现相机落在途中了,妈妈立即返回找相机,小亮继续前往长嘉汇,当小亮到达长嘉汇时,妈妈刚好找到了相机并立即前往长嘉汇(妈妈找相机的时间不计),小亮在长嘉汇等了一会,没有等到妈妈,就沿同一路线返回接妈妈,最终与妈妈会合,小亮和妈妈的速度始终不变,如图是小亮和妈妈两人之间的距离y(米)与妈妈出发的时间x(分钟)的图象;则小亮开始返回时,妈妈离家的距离为_____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于点E,连接CE.
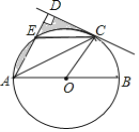
(1)判断CD与⊙O的位置关系,并证明你的结论;
(2)若E是弧AC的中点,⊙O的半径为2,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
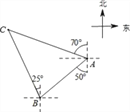
【题目】如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )
A. 10![]() 海里 B. 10
海里 B. 10![]() 海里 C. 10
海里 C. 10![]() 海里 D. 20
海里 D. 20![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 在![]() .
.
(1)用尺规作图方法,按要求作图:
①作![]() 的高
的高![]() ;
;
②作![]() 的平分线
的平分线![]() ,分别交
,分别交![]() 于点
于点![]() ;
;
(要求:保留作图痕迹,不写作法和证明)
(2)求证:点![]() 在
在![]() 的垂直平分线.上; .
的垂直平分线.上; .
(3)在(1)所作的图中,探究线段AE与BF的数量关系,并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com