
【题目】如图, 在![]() .
.
(1)用尺规作图方法,按要求作图:
①作![]() 的高
的高![]() ;
;
②作![]() 的平分线
的平分线![]() ,分别交
,分别交![]() 于点
于点![]() ;
;
(要求:保留作图痕迹,不写作法和证明)
(2)求证:点![]() 在
在![]() 的垂直平分线.上; .
的垂直平分线.上; .
(3)在(1)所作的图中,探究线段AE与BF的数量关系,并证明你的结论.

【答案】(1)①见解析;②见解析;(2)证明见解析;(3)AE=2BF,证明见解析.
【解析】
(1)根据过已知直线外一点垂线的步骤作图;
(2)根据作角平分线的步骤作图;
(3)根据到线段两端点距离相等的点在线段的垂直平分线上,证明DA=DB即可;
(4)通过证△ADE≌△BDC得出AE=BC,再根据等腰三角形三线合一的性质得出BC=2BF即可得出结论.
(1)①如图1,以B为圆心,BC为半径画弧,交AC于M;以C、M分别为圆心,以大于![]() 为半径画弧,两弧交于点P;作射线BP交AC于D,线段BD就是要求作的△ABC的高;
为半径画弧,两弧交于点P;作射线BP交AC于D,线段BD就是要求作的△ABC的高;
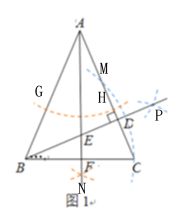
② 如图1,以A为圆心,以任意长为半径画弧,交AB,AC于G,H;以G,H分别为圆心,以大于![]() 为半径画弧,两弧交于N点;作射线AN,交BC于F点,射线AF就是所要求作的∠BAC的平分线;
为半径画弧,两弧交于N点;作射线AN,交BC于F点,射线AF就是所要求作的∠BAC的平分线;
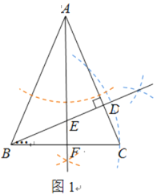
(2)∵∠BAC=45°,∠ADB=90°,
∴ ∠ABD=∠BAC=45°.
∴ DA=DB,
∴ 点D在AB的垂直平分线上.
 …
…
(3)∵ AB=AC,AF是∠BAC的角平分线,
∴ BC=2BF,AF⊥BC.
∴ ∠DAF+∠C=90°.
∵ ∠DBC+∠C=90°,
∴ ∠DAE=∠DBC.
又 ∵ DA=DB,∠ADE=∠BDC=90°,
∴ △ADE≌△BDC (ASA).
∴ AE=BC,
∴ AE=2BF.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,AB=2,AD和BE是圆O的两条切线,A,B为切点,过圆上一点C作⊙O的切线CF,分别交AD,BE于点M,N,连接AC,CB.若∠ABC=30°,则AM等于( )

A. 0.5 B. 1 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)
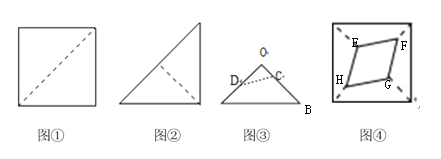
将一张正方形纸片按如图步骤①②,沿虚线对折2次,然后沿图③的虚线剪去一个角,展开铺平后得到图④,若图③中![]() ,
,![]() ,则四边形
,则四边形![]() 与原正方形纸面积比为( )
与原正方形纸面积比为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D,E,F分别是△ABC三边的中点,则下列判断错误的是( )
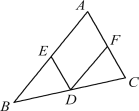
A. 四边形AEDF一定是平行四边形 B. 若AD平分∠A,则四边形AEDF是正方形
C. 若AD⊥BC,则四边形AEDF是菱形 D. 若∠A=90°,则四边形AEDF是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两位老师同住一小区,该小区与学校相距![]() 米.甲从小区步行去学校,出发
米.甲从小区步行去学校,出发![]() 分钟后乙再出发,乙从小区先骑公共自行车,骑行若干米到达还车点后,立即步行走到学校.已知乙骑车的速度为
分钟后乙再出发,乙从小区先骑公共自行车,骑行若干米到达还车点后,立即步行走到学校.已知乙骑车的速度为![]() 米/分,甲步行的速度比乙步行的速度每分钟快
米/分,甲步行的速度比乙步行的速度每分钟快![]() 米.设甲步行的时间为
米.设甲步行的时间为![]() (分),图1中线段
(分),图1中线段![]() 与折线
与折线![]() 分别表示甲、乙离小区的路程
分别表示甲、乙离小区的路程![]() (米)与甲步行时间
(米)与甲步行时间![]() (分)的函数关系的图象;图2表示甲、乙两人之间的距离
(分)的函数关系的图象;图2表示甲、乙两人之间的距离![]() (米)与甲步行时间
(米)与甲步行时间![]() (分)的函数关系的图象(不完整),根据图1和图2中所给的信息,解答下列问题:
(分)的函数关系的图象(不完整),根据图1和图2中所给的信息,解答下列问题:
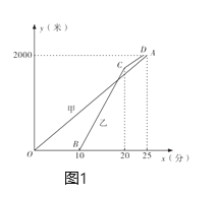
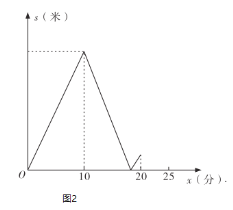
(1)求甲步行的速度和乙出发时甲离开小区的路程;
(2)求直线![]() 的解析式;
的解析式;
(3)在图2中,画出当![]() 时,
时,![]() 关于
关于![]() 的函数的大致图象.
的函数的大致图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]()
(2)(﹣![]() a6x5y4)÷(﹣3a2xy2)×(﹣
a6x5y4)÷(﹣3a2xy2)×(﹣![]() ax)2
ax)2
(3)[(x﹣2y)2+(x﹣2y)(x+2y)﹣2x(2x﹣y)]÷2x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com