
 如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路.
如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路.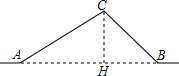 解:(1)作CH⊥AB于H.
解:(1)作CH⊥AB于H.

科目:初中数学 来源: 题型:
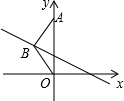 如图,等腰三角形ABO中,底边OA在y轴的正半轴上,且OA=3,点B在第二象限.若直线y=-
如图,等腰三角形ABO中,底边OA在y轴的正半轴上,且OA=3,点B在第二象限.若直线y=-| 1 |
| 2 |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
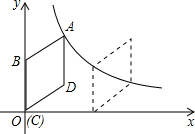 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的| k |
| x |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
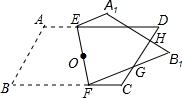 如图,将?ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在点A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD,DE于点H,I.求证:EI=FG.
如图,将?ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在点A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD,DE于点H,I.求证:EI=FG.查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |
| 5 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com