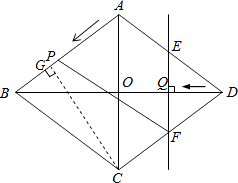
【题目】已知：如图，在菱形ABCD中，对角线AC，BD相交于点O，且AC=12cm，BD=16cm．点P从点A出发，沿AB方向匀速运动，速度为1cm/s；过点P作直线PF∥AD，PF交CD于点F，过点F作EF⊥BD，且与AD、BD分别交于点E、Q；连接PE，设点P的运动时间为t（s）（0＜t＜10）．
解答下列问题：
（1）填空：AB= cm；
（2）当t为何值时，PE∥BD；
（3）设四边形APFE的面积为y（cm2）
①求y与t之间的函数关系式；
②若用S表示图形的面积，则是否存在某一时刻t，使得S四边形APFE= S菱形ABCD？若存在，求出t的值；若不存在，请说明理由．

参考答案：

【答案】
（1）10
（2）解：∵在菱形ABCD中，∴AB∥CD，∠ADB=∠CDB，

又∵PF∥AD，

∴四边形APFD为平行四边形，

∴DF=AP=t，

又∵EF⊥BD于Q，且∠ADB=∠CDB，

∴∠DEF=∠DFE，

∴DE=DF=t，

∴AE=10﹣t，

当PE∥BD时，△APE∽△ABD，

∴ ，

∴ ，

∴t=5，

∴当t=5时，PE∥BD


（3）蛸：①∵∠FDQ=∠CDO，∠FQD=∠COD=90°，

∴△DFQ∽△DCO．

∴ ，

即 ，

∴ ．

∴ ，

同理， ，

如图，过点C作CG⊥AB于点G，

∵S菱形ABCD=ABCG= ACBD，

即10CG= ×12×16，

∴CG= ．

∴S平行四边形APFD=DFCG= ，

∴S△EFD= EFQD=

∴ ，

②当S四边形APFE= S菱形ABCD

则 ，

即t2﹣20t+64=0，

解这个方程，得t1=4，t2=16＞10（不合，舍去）

∴存在t=4s，使得S四边形APFE= S菱形ABCD．


【解析】解：（1）∵在菱形ABCD中，对角线AC，BD相交于点O，且AC=12cm，BD=16cm，

∴BO=DO=8cm，AO=CO=6cm，

∴AB= =10（cm），

所以答案是：10；


【考点精析】解答此题的关键在于理解因式分解法的相关知识，掌握已知未知先分离，因式分解是其次．调整系数等互反，和差积套恒等式．完全平方等常数，间接配方显优势，以及对平行四边形的判定与性质的理解，了解若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段以对角线的交点为中点，并且这两条直线二等分此平行四边形的面积．

关闭