
【题目】设m是不小于﹣1的实数,使得关于x的方程x2+2(m﹣2)x+m2﹣3m+3=0有两个实数根x1 , x2 .
(1)若x12+x22=2,求m的值;
(2)代数式 ![]() +
+ ![]() 有无最大值?若有,请求出最大值;若没有,请说明理由.
有无最大值?若有,请求出最大值;若没有,请说明理由.
【答案】
(1)解:根据题意得△=4(m﹣2)2﹣4(m2﹣3m+3)≥0,解得m≤1,
∵m是不小于﹣1的实数
∴﹣1≤m≤1,
x1+x2=﹣2(m﹣2),x1x2=m2﹣3m+3,
∵x12+x22=2,
∴(x1+x2)2﹣2x1x2=2,
∴4(m﹣2)2﹣2(m2﹣3m+3)=2,
整理得m2﹣5m+4=0,解得m1=1,m2=4(舍去),
∴m的值为1
(2)解:代数式有最大值.理由如下:
![]() +
+ ![]() =m
=m ![]() =m
=m ![]() =m
=m ![]() =﹣2m+2,
=﹣2m+2,
∴﹣1≤m≤1且m≠0,m≠1,
∴当m=﹣1时,代数式的值最大,最大值为4
【解析】(1)根据方程有两个实数根知△=4(m﹣2)2﹣4(m2﹣3m+3)≥0,解得m≤1,又m是不小于﹣1的实数,从而得出m的取值范围﹣1≤m≤1,将方程x12+x22=2变形为(x1+x2)2﹣2x1x2=2,根据根与系数之间的关系得x1+x2=-2(m﹣2),x1x2=m2﹣3m+3,整体代入得出一个关于m的方程求解得出解得m1=1,m2=4(舍去),从而得出m的值;
(2)代数式有最大值.理由如下:将代数式通分合并,整体代入化简得出原式=﹣2m+2,又﹣1≤m≤1且m≠0,m≠1,故当m=﹣1时,代数式的值最大,最大值为4
【考点精析】认真审题,首先需要了解因式分解法(已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势),还要掌握求根公式(根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根)的相关知识才是答题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠A=30°,∠B=60°。
(1)作∠B的平分线BD,交AC于点D;作AB的中点E(要求:尺规作图,保留作图痕迹)
(2)连接DE,求证:△ADE≌△BDE。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在矩形ABCD中,E是BC上一点,AF⊥DE于点F.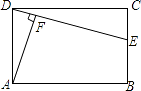
(1)求证:DFCD=AFCE.
(2)若AF=4DF,CD=12,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
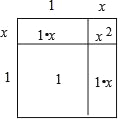
【题目】(1)下面是李老师带领同学们探索![]() 的近似值的过程,请你仔细阅读并补充完整:我们知道,面积是2的正方形的边长是
的近似值的过程,请你仔细阅读并补充完整:我们知道,面积是2的正方形的边长是![]() ,且
,且![]() >1,则设
>1,则设![]() =1+x(0<x<1),可画出如图所示的示意图.由各部分面积之和等于总面积.可列方程为:x2+ +1=2,∵0<x<1,∴认为x2是个较为接近于0的数,令x2≈0,因此省略x2后,得到方程: ,解得,x= ,即
=1+x(0<x<1),可画出如图所示的示意图.由各部分面积之和等于总面积.可列方程为:x2+ +1=2,∵0<x<1,∴认为x2是个较为接近于0的数,令x2≈0,因此省略x2后,得到方程: ,解得,x= ,即![]() =1+x≈ .
=1+x≈ .
(2)请仿照(1)中的方法,若设![]() =1.7+y(0<y<1),求
=1.7+y(0<y<1),求![]() 的近似值(要求画出示意图,标明数据,并将
的近似值(要求画出示意图,标明数据,并将![]() 的近似值精确到千分位)
的近似值精确到千分位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点A出发,沿AB方向匀速运动,速度为1cm/s;过点P作直线PF∥AD,PF交CD于点F,过点F作EF⊥BD,且与AD、BD分别交于点E、Q;连接PE,设点P的运动时间为t(s)(0<t<10).![]() 解答下列问题:
解答下列问题:
(1)填空:AB= cm;
(2)当t为何值时,PE∥BD;
(3)设四边形APFE的面积为y(cm2)
①求y与t之间的函数关系式;
②若用S表示图形的面积,则是否存在某一时刻t,使得S四边形APFE= ![]() S菱形ABCD?若存在,求出t的值;若不存在,请说明理由.
S菱形ABCD?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的线段AB及点P,给出如下定义:
若点P满足PA=PB,则称P为线段AB的“轴点”,其中,当0°<∠APB<60°时,称P为线段AB的“远轴点”;当60°≤∠APB≤180°时,称P为线段AB的“近轴点”.
(1)如图1,点A,B的坐标分别为(-2,0),(2,0),则在![]() ,
,![]() ,
,![]() ,
,![]() 中,线段AB的“近轴点”是 .
中,线段AB的“近轴点”是 .
(2)如图2,点A的坐标为(3,0),点B在y轴正半轴上,且∠OAB=30°.
①若P为线段AB的“远轴点”,直接写出点P的横坐标t的取值范围 ;
②点C为y轴上的动点(不与点B重合且BC≠AB),若Q为线段AB的“轴点”,当线段QB与QC的和最小时,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算并观察下列各式:
第1个:(a﹣b)(a+b)=______;
第2个:(a﹣b)(a2+ab+b2)=______;
第3个:(a﹣b)(a3+a2b+ab2+b3)=_______;
……
这些等式反映出多项式乘法的某种运算规律.
(2)猜想:若n为大于1的正整数,则(a﹣b)(an﹣1+an﹣2b+an﹣3b2+……+a2bn﹣3+abn﹣2+bn﹣1)=________;
(3)利用(2)的猜想计算:2n﹣1+2n﹣2+2n﹣3+……+23+22+1=______.
(4)拓广与应用:3n﹣1+3n﹣2+3n﹣3+……+33+32+1=_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com