
【题目】如图所示,在矩形ABCD中,E是BC上一点,AF⊥DE于点F.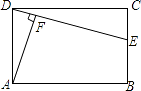
(1)求证:DFCD=AFCE.
(2)若AF=4DF,CD=12,求CE的长.
【答案】
(1)证明:
∵四边形ABCD是矩形,
∴∠ADC=∠C=90°,
∴∠ADF+∠CDE=90°,
∵AF⊥DE,
∴∠AFD=∠DAF+∠FDA=90°,
∴∠FAD=∠CDE,
又∵∠C=∠AFD=90°,
∴△ADF∽△DCE;
∴ ![]() ,
,
即DFCD=AFCE
(2)解:∵△ADF∽△DCE;
∴ ![]() ,
,
∴ ![]()
![]() ,
,
又∵AF=4DF,CD=12,
∴ ![]() ,
,
∴CE=3.
【解析】(1)根据矩形的性质得出∠ADC=∠C=90°,根据同角的余角相等得出∠FAD=∠CDE,进而判断出△ADF∽△DCE;根据相似三角形对应边成比例得出结论;
(2)根据根据相似三角形对应边成比例得出![]() =
=![]() ,根据比例的性质得出
,根据比例的性质得出![]() =
=![]() ,将AF=4DF,CD=12,代入即可求出CE的长。
,将AF=4DF,CD=12,代入即可求出CE的长。
【考点精析】本题主要考查了矩形的性质和比例的性质的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等;基本性质;更比性质(交换比例的内项或外项);反比性质(交换比的前项、后项);等比性质才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】小明的父母出去散步,从家走了20分钟到一个离家900米的报亭,母亲随即按原速度返回家,父亲在报亭看了10分钟报纸后,用15分钟返回家,则表示父亲、母亲离家距离与时间之间的关系是(只需填序号). 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,所有小正方形的边长都为1,A、B、C都在格点上.
(1)过点C画直线AB的平行线(不写画法,下同);
(2)过点A画直线BC的垂线,并注明垂足为G;过点A画直线AB的垂线,交BC于点H.
(3)线段_____的长度是点A到直线BC的距离;
(4)线段AG、AH的大小关系为AG_____AH.(填“>”或“<”或“=”),理由________.

查看答案和解析>>
科目:初中数学 来源: 题型:
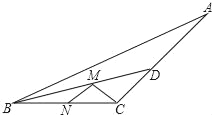
【题目】如图,钝角三角形△ABC的面积是15,最长边AB=10,BD平分∠ABC,点M,N分别是BD,BC上的动点,则CM+MN的最小值为_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,∠C=∠D。
求证:∠A=∠F。

证明:∵∠1=∠2(已知),
又∠1=∠DMN(_______________),
∴∠2=∠_________(等量代换),
∴DB∥EC( ),
∴∠DBC+∠C=1800(两直线平行 , ),
∵∠C=∠D( ),
∴∠DBC+ =1800(等量代换),
∴DF∥AC( ,两直线平行),
∴∠A=∠F( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设m是不小于﹣1的实数,使得关于x的方程x2+2(m﹣2)x+m2﹣3m+3=0有两个实数根x1 , x2 .
(1)若x12+x22=2,求m的值;
(2)代数式 ![]() +
+ ![]() 有无最大值?若有,请求出最大值;若没有,请说明理由.
有无最大值?若有,请求出最大值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC向右平移3个单位长度,再向上平移2个单位长度,得到△A′B′C′,点A(-1,2),B(-3,1),C(0,-1)的对应点分别是A′,B′,C′.
(1)在图中画出△A′B′C′;
(2)分别写出点A′,B′,C′的坐标;
(3)求△A′B′C′的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】创建文明城市,人人参与,人人共建.我市各校积极参与创建活动,自发组织学生走上街头,开展文明劝导活动.某中学九(一)班为此次活动制作了大小、形状、质地等都相同的“文明劝导员”胸章和“文明监督岗”胸章若干,放入不透明的盒中,此时从盒中随机取出“文明劝导员”胸章的概率为 ![]() ;若班长从盒中取出“文明劝导员”胸章3只、“文明监督岗”胸章7只送给九(二)班后,这时随机取出“文明劝导员”胸章的概率为
;若班长从盒中取出“文明劝导员”胸章3只、“文明监督岗”胸章7只送给九(二)班后,这时随机取出“文明劝导员”胸章的概率为 ![]() .
.
(1)请你用所学知识计算:九(一)班制作的“文明劝导员”胸章和“文明监督岗”胸章各有多少只?
(2)若小明一次从盒内剩余胸章中任取2只,问恰有“文明劝导员”胸章、“文明监督岗”胸章各1只的概率是多少?(用列表法或树状图计算)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com