
【题目】创建文明城市,人人参与,人人共建.我市各校积极参与创建活动,自发组织学生走上街头,开展文明劝导活动.某中学九(一)班为此次活动制作了大小、形状、质地等都相同的“文明劝导员”胸章和“文明监督岗”胸章若干,放入不透明的盒中,此时从盒中随机取出“文明劝导员”胸章的概率为 ![]() ;若班长从盒中取出“文明劝导员”胸章3只、“文明监督岗”胸章7只送给九(二)班后,这时随机取出“文明劝导员”胸章的概率为
;若班长从盒中取出“文明劝导员”胸章3只、“文明监督岗”胸章7只送给九(二)班后,这时随机取出“文明劝导员”胸章的概率为 ![]() .
.
(1)请你用所学知识计算:九(一)班制作的“文明劝导员”胸章和“文明监督岗”胸章各有多少只?
(2)若小明一次从盒内剩余胸章中任取2只,问恰有“文明劝导员”胸章、“文明监督岗”胸章各1只的概率是多少?(用列表法或树状图计算)
【答案】
(1)解:九(一)班制作的“文明劝导员”胸章和“文明监督岗” 胸章分别为x只、y只,
根据题意得:  解得:
解得: ![]() 经检验符合题意,
经检验符合题意,
所以九(一)班制作了“文明劝导员” 胸章5只、“文明监督岗” 胸章10只
(2)解:由题可知,盒中剩余的“文明劝导员” 胸章和“文明监督岗” 胸章分别为2只、3只,我们不妨把两只“文明劝导员” 胸章记为a1、a2;3只“文明监督岗” 胸章记为b1、b2、b3,则可列出表格如下:
a1 | a2 | b1 | b2 | b3 | |
a1 | a1 a2 | a1b1 | a1b2 | a1b3 | |
a2 | a2 a1 | a2 b1 | a2 b2 | a2 b3 | |
b1 | b1 a1 | b1a2 | b1 b2 | b1 b3 | |
b2 | b2 a1 | b2a2 | b2b1 | b2 b3 | |
b3 | b3 a1 | b3a2 | b3b1 | b3b2 |
∴ ![]()
【解析】(1)九(一)班制作的“文明劝导员”胸章和“文明监督岗” 胸章分别为x只、y只,根据概率公式由前后两次概率的值列出二元一次方程组,求解检验即可;
(2)由题可知,盒中剩余的“文明劝导员” 胸章和“文明监督岗” 胸章分别为2只、3只,我们不妨把两只“文明劝导员” 胸章记为a1、a2;3只“文明监督岗” 胸章记为b1、b2、b3,则可列出表格,由表格可知所有均可能结果共20种,其中文明劝导员”胸章、“文明监督岗”胸章各1只的情况共12种,根据概率公式计算即可。
【考点精析】认真审题,首先需要了解列表法与树状图法(当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率),还要掌握概率公式(一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n)的相关知识才是答题的关键.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在矩形ABCD中,E是BC上一点,AF⊥DE于点F.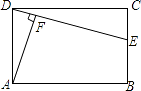
(1)求证:DFCD=AFCE.
(2)若AF=4DF,CD=12,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算并观察下列各式:
第1个:(a﹣b)(a+b)=______;
第2个:(a﹣b)(a2+ab+b2)=______;
第3个:(a﹣b)(a3+a2b+ab2+b3)=_______;
……
这些等式反映出多项式乘法的某种运算规律.
(2)猜想:若n为大于1的正整数,则(a﹣b)(an﹣1+an﹣2b+an﹣3b2+……+a2bn﹣3+abn﹣2+bn﹣1)=________;
(3)利用(2)的猜想计算:2n﹣1+2n﹣2+2n﹣3+……+23+22+1=______.
(4)拓广与应用:3n﹣1+3n﹣2+3n﹣3+……+33+32+1=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学重要的著作之一,奠定了中国传统数学的基本框架.其中第九卷《勾股》主要讲述了以测量问题为中心的直角三角形三边互求,之中记载了一道有趣的“引葭赴岸”问题:“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长各几何?”
译文:“今有正方形水池边长为1丈,有棵芦苇生长在它长出水面的部分为1尺.将芦苇的中央,向池岸牵引,恰好与水岸齐接.问水深,芦苇的长度分别是多少尺?”(备注:1丈=10尺)
如果设水深为![]() 尺,那么芦苇长用含
尺,那么芦苇长用含![]() 的代数式可表示为_______尺,根据题意,可列方程为______________.
的代数式可表示为_______尺,根据题意,可列方程为______________.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红根据学习“数与式”积累的经验,想通过“由特殊到一般”的方法探究下面二次根式的运算规律.
下面是小红的探究过程,请补充完整:
(1)具体运算,发现规律.
特例1:![]() ,
,
特例2:![]() ,
,
特例3:![]() ,
,
特例4: (填写一个符合上述运算特征的例子).
(2)观察、归纳,得出猜想.
如果![]() 为正整数,用含
为正整数,用含![]() 的式子表示上述的运算规律为: .
的式子表示上述的运算规律为: .
(3)证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小彬买了A、B两种书,单价分别是18元、10元.
(1)若两种书共买了10本付款172元,求每种书各买了多少本?
(2)买10本时付款可能是123元吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上点A对应的数为a,点B对应的数为b,且多项式﹣![]() x2y﹣
x2y﹣![]() xy2﹣2xy+5的次数为a,常数项为b.
xy2﹣2xy+5的次数为a,常数项为b.
(1)直接写出a、b的值;
(2)数轴上点A、B之间有一动点P(不与A、B重合),若点P对应的数为x,试化简:|2x+6|+4|x﹣5|﹣|6﹣x|+|3x﹣9|.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(给出定义)
数轴上顺次有三点A、C、B,若点C到点A的距离是点C到点B的距离的3倍,我们就称点C是(A、B)的“梦想点”例如:图①中,点A、B表示的数分别为-2、2,表示数1的点C是(A、B)的“梦想点”;图②中,点A、B表示对的数分别为-2、2,表示-1的点C是(B、A)的“梦想点.

(解决问题)
(1)若数轴上M、N两点所表示的数分别为![]() 且
且![]() 满足
满足![]() 求出(M、N)的“梦想点”表示的数;
求出(M、N)的“梦想点”表示的数;
(2)如图③,在数轴上点A、B表示的数分别为-15和65,点P从点A出发沿数轴向右运动:
①若点P运动到点B停止,则当P、A、B中恰好有一个点为其余两个点的“梦想点”时,求这个点表示的数;
②若点P运动到B后,继续沿数轴向右运动的过程中,是否还存在点P、A、B中恰好有一个点为其余两点的“梦想点”的情况?若存在,请直接写出此时以PA、PB为邻边长的长方形的周长;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com