Question

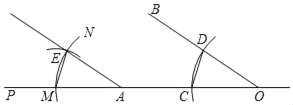
【题目】已知C是线段AB垂直平分线m上一动点，连接AC，以AC为边作等边三角形ACD，点D在直线AB的上方，连接DB与直线m交于点E，连接BC，AE．

(1)如图1，点C在线段AB上．

①根据题意补全图1；

②求证：∠EAC=∠EDC；

(2)如图2，点C在直线AB的上方， 0°＜∠CAB＜30°，用等式表示线段BE，CE，DE之间的数量关系，并证明．

Answer 1

【答案】(1)①补全图形见解析；②证明见解析；(2)BE=CE+DE，证明见解析.

【解析】

（1）①根据题意补全图形即可；②根据垂直平分线的性质可得EA＝EB，CA＝CB，根据等边三角形的性质可得CA＝CD，因此CD＝CB，即可证得∠EDC＝∠B；（2）如图，在EB上截取EF，使EF=CE，连接CF．根据垂直平分线的性质以及等边三角形的性质可推出∠EDC＝∠EAC，又因为∠1＝∠2，可得∠DEA＝60°，所以∠AEB＝120°，进而可推出△CEF是等边三角形，因此△CDF≌△CBE，故BE＝DF＝CE＋DE.

(1)①补全图形如图所示．

②∵直线m是AB的垂直平分线，

∴EA=EB，CA=CB．

∴∠EAC=∠B．

∵△ACD是等边三角形，

∴CA=CD．

∴CD=CB．

∴∠EDC=∠B．

∴∠EAC=∠EDC．

(2)BE=CE+DE．

如图，在EB上截取EF，使EF=CE，连接CF．

∵直线m是AB的垂直平分线，

∴EA=EB，CA=CB．

∴∠EAB=∠EBA，∠CAB=∠CBA．

∴∠EAC=∠EBC．

∵△ACD是等边三角形，

∴CA=CD，∠ACD=60°．

∴CD=CB．

∴∠EDC=∠EBC．

∴∠EDC=∠EAC．

∵∠1=∠2，

∴∠DEA=∠ACD=60°．

∴∠AEB=120°．

∵EA=EB，m⊥AB，

∴∠AEC=∠BEC=60°．

∴△CEF是等边三角形．

∴∠CEF=∠CFE=60°．

∴△CDF≌△CBE．

∴DF=BE．

∴BE=CE+DE．