
【题目】如图,将圆心角都是90°的扇形OAB和扇形OCD叠放在一起,连接AC、BD.
(1)将△AOC经过怎样的图形变换可以得到△BOD?
(2)若 ![]() 的长为πcm,OD=3cm,求图中阴影部分的面积是多少?
的长为πcm,OD=3cm,求图中阴影部分的面积是多少?
【答案】
(1)解:∵扇形OAB和扇形OCD的圆心角都是90°,
∴OA=OB,OC=OD,∠AOB=∠COD=90°,
∴将△AOC绕点O顺时针旋转90°可以得到△BOD
(2)解:∵ ![]() =π,
=π,
∴OA=2,
∵△AOC绕点O顺时针旋转90°可以得到△BOD,
∴△AOC≌△BOD,
∴S△AOC=S△BOD,
∵S△AOC+S扇形COD=S△BOD+S扇形AOB+S阴影部分,
∴S阴影部分=S扇形COD﹣S扇形AOB= ![]() ﹣
﹣ ![]() =
= ![]() π(cm2)
π(cm2)
【解析】(1)扇形OAB和扇形OCD的圆心角都是90°,OA=OB,OC=OD,∠AOB=∠COD=90°,从而能判断出△AOC![]() △BOD ,根据旋转的性质知 将△AOC绕点O顺时针旋转90°可以得到△BOD;
△BOD ,根据旋转的性质知 将△AOC绕点O顺时针旋转90°可以得到△BOD;
(2)根据弧长计算公式及弧A B 的长度建立方程,从而求出OA的长,又由于△AOC≌△BOD,根据全等三角形的面积相等得出S△AOC=S△BOD,然后根据S△AOC+S扇形COD=S△BOD+S扇形AOB+S阴影部分,得S阴影部分=S扇形COD﹣S扇形AOB,算出答案。
【考点精析】解答此题的关键在于理解弧长计算公式的相关知识,掌握若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的,以及对扇形面积计算公式的理解,了解在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).


科目:初中数学 来源: 题型:
【题目】如图①,某超市从一楼到二楼有一自动扶梯,图②是侧面示意图.已知自动扶梯AB的坡度为1∶2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ , C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN , 在自动扶梯底端A处测得C点的仰角为42°,则二楼的层高BC约为(精确到0.1米,sin42°≈0.67,tan42°≈0.90)( )
A.10.8米
B.8.9米
C.8.0米
D.5.8米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,∠C=∠D。
求证:∠A=∠F。

证明:∵∠1=∠2(已知),
又∠1=∠DMN(_______________),
∴∠2=∠_________(等量代换),
∴DB∥EC( ),
∴∠DBC+∠C=1800(两直线平行 , ),
∵∠C=∠D( ),
∴∠DBC+ =1800(等量代换),
∴DF∥AC( ,两直线平行),
∴∠A=∠F( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知C是线段AB垂直平分线m上一动点,连接AC,以AC为边作等边三角形ACD,点D在直线AB的上方,连接DB与直线m交于点E,连接BC,AE.
(1)如图1,点C在线段AB上.
①根据题意补全图1;
②求证:∠EAC=∠EDC;
(2)如图2,点C在直线AB的上方, 0°<∠CAB<30°,用等式表示线段BE,CE,DE之间的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC向右平移3个单位长度,再向上平移2个单位长度,得到△A′B′C′,点A(-1,2),B(-3,1),C(0,-1)的对应点分别是A′,B′,C′.
(1)在图中画出△A′B′C′;
(2)分别写出点A′,B′,C′的坐标;
(3)求△A′B′C′的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是Rt△ABC的外接圆,∠ACB=90°,AC平分∠BAD,CD⊥AD于D,AD交⊙O于E.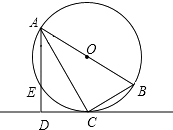
(1)求证:CD为⊙O的切线;
(2)若⊙O的直径为8cm,CD=2 ![]() cm,求弦AE的长.
cm,求弦AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点E是AC上的点,且∠1=∠2,DE垂直平分AB,垂足是D,如果EC=3 cm,那么AE等于( )
A.3 cm
B.![]() cm
cm
C.6 cm
D.![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com