
【题目】当x满足条件  时,求出方程x2﹣2x﹣4=0的根.
时,求出方程x2﹣2x﹣4=0的根.
【答案】解:由 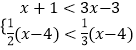 求得
求得 ![]() ,则2<x<4.
,则2<x<4.
解方程x2﹣2x﹣4=0可得x1=1+ ![]() ,x2=1﹣
,x2=1﹣ ![]() ,∵2<
,∵2< ![]() <3,∴3<1+
<3,∴3<1+ ![]() <4,符合题意
<4,符合题意
∴x=1+ ![]() .
.
【解析】分别解出不等式中的每一个不等式,然后利用大小小大中间找得出求出不等式组的解积;然后解出方程x2﹣2x﹣4=0的解,然后根据x的取值范围判断即可。
【考点精析】掌握配方法和一元一次不等式组的解法是解答本题的根本,需要知道左未右已先分离,二系化“1”是其次.一系折半再平方,两边同加没问题.左边分解右合并,直接开方去解题;解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ).


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】已知∠BOP与OP上点C,点A(在A的左侧),嘉嘉进行如下作图:
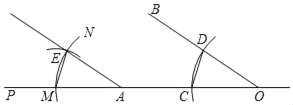
①以点O为圆心,OC为半径画弧,交OB于点D,连接CD
②以点A为圆心,OC为半径画弧MN,交AP于点M
③以点M为圆心,CD为半径画弧,交MN于点E,连接ME,作射线AE
如图所示,则下列结论不成立的是( )
A. CD∥EM B. AE∥OB C. ∠ODC=∠AEM D. ∠OAE=∠BDC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将圆心角都是90°的扇形OAB和扇形OCD叠放在一起,连接AC、BD.
(1)将△AOC经过怎样的图形变换可以得到△BOD?
(2)若 ![]() 的长为πcm,OD=3cm,求图中阴影部分的面积是多少?
的长为πcm,OD=3cm,求图中阴影部分的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量校园内一棵不可攀的树的高度,数学应用实践小组做了如下的探索实践:根据《物理学》中光的反射定律,利用一面镜子和一根皮尺,设计如图的测量方案:把镜子放在离树(AB)9米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.7米,观察者目高CD=1.8米,则树(AB)的高度为米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学重要的著作之一,奠定了中国传统数学的基本框架.其中第九卷《勾股》主要讲述了以测量问题为中心的直角三角形三边互求,之中记载了一道有趣的“引葭赴岸”问题:“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长各几何?”
译文:“今有正方形水池边长为1丈,有棵芦苇生长在它长出水面的部分为1尺.将芦苇的中央,向池岸牵引,恰好与水岸齐接.问水深,芦苇的长度分别是多少尺?”(备注:1丈=10尺)
如果设水深为![]() 尺,那么芦苇长用含
尺,那么芦苇长用含![]() 的代数式可表示为_______尺,根据题意,可列方程为______________.
的代数式可表示为_______尺,根据题意,可列方程为______________.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.
(1)证明不论E、F在BC.CD上如何滑动,总有BE=CF;
(2)当点E、F在BC.CD上滑动时,分别探讨四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小彬买了A、B两种书,单价分别是18元、10元.
(1)若两种书共买了10本付款172元,求每种书各买了多少本?
(2)买10本时付款可能是123元吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学进行社会调查,随机抽查了某个地区的20个家庭的收入情况,并绘制了统计图,请你根据统计图给出的信息回答:

(1)填写完成下表:
年收入(万元) | 0.6 | 0.9 | 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 9.7 |
户 数 | 1 | 1 | 2 | 4 |
这20个家庭的年平均收入为 万元;
(2)样本中的中位数是 万元,众数是 万元;
(3)在平均数、中位数两数中, 更能反映这个地区家庭的年收入水平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是

A.4 B.3 C.2 D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com