
【题目】如图,已知⊙O是Rt△ABC的外接圆,∠ACB=90°,AC平分∠BAD,CD⊥AD于D,AD交⊙O于E.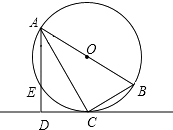
(1)求证:CD为⊙O的切线;
(2)若⊙O的直径为8cm,CD=2 ![]() cm,求弦AE的长.
cm,求弦AE的长.
【答案】
(1)证明:连接OC,如图所示:
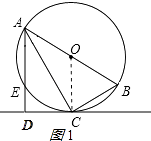
∵OA=OC,
∴∠OAC=∠0CA,
∵AC平分∠BAD,
∴∠OAC=∠CAD,
∴∠CAD=∠ACO,
∴OC∥AD,
∵CD⊥AD,
∴CD⊥OC,
∴CD为⊙O的切线;
(2)解:作OF⊥AE于F,如图2所示:
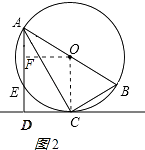
则AF= ![]() AE,四边形OFDC是矩形,
AE,四边形OFDC是矩形,
∴OF=CD=2 ![]() cm,
cm,
∵OA= ![]() AB=4cm,
AB=4cm,
∴AF= ![]() =
= ![]() =2,
=2,
∴AE=2AF=4.
【解析】(1)连接OC,根据等边对等角,角平分线的定义及等量代换得出∠CAD=∠ACO,从而根据内错角相等两直线平行得出OC∥AD,然后根据平行线的性质得出CD⊥OC,即CD为⊙O的切线;
(2)作OF⊥AE于F,根据垂径定理得出得出AF=![]() AE,根据三个角是直角得四边形是矩形得出四边形OFDC是矩形,根据矩形的对边相等得出OF=CD,然后利用勾股定理得出AF的长,从而得出AE的长。
AE,根据三个角是直角得四边形是矩形得出四边形OFDC是矩形,根据矩形的对边相等得出OF=CD,然后利用勾股定理得出AF的长,从而得出AE的长。
【考点精析】通过灵活运用平行线的判定与性质和垂径定理,掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧即可以解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
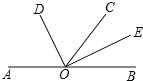
【题目】如图,点A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)当∠BOE=25°时,求∠AOD的度数
(2)在图中找出∠COD的补角,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角” (如图)就是一例.这个三角形给出了![]() (n=1,2,3,4,5,6)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应
(n=1,2,3,4,5,6)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应![]() 展开式中各项的系数;第五行的五个数1,4,6,4,1,恰好对应着
展开式中各项的系数;第五行的五个数1,4,6,4,1,恰好对应着![]() 展开式中各项的系数,等等.
展开式中各项的系数,等等.

有如下三个结论:
①当a=1,b=1时,代数式![]() 的值是1;
的值是1;
②当a=-1,b=2时,代数式![]() 的值是1;
的值是1;
③当代数式![]() 的值是1时,a的值是-2或-4.
的值是1时,a的值是-2或-4.
上述结论中,所有正确结论的序号为( )
A. ①② B. ② C. ③ D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售同一品牌羽绒服和防寒服,已知去年12月份,销售羽绒服a件,防寒服销量是羽绒服的4倍,其中防寒服售价为b元/件,羽绒服的售价是防寒服的4倍,受市场影响,今年1月份,羽绒服销量和售价均下降m%,但防寒服销量和售价均增加m%.
(1)求该商场今年1月份销售羽绒服和防寒服的销售额;
(2)若a=100,b=300,m=5,则该商场今年1月份销售羽绒服和防寒服的销售额是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将圆心角都是90°的扇形OAB和扇形OCD叠放在一起,连接AC、BD.
(1)将△AOC经过怎样的图形变换可以得到△BOD?
(2)若 ![]() 的长为πcm,OD=3cm,求图中阴影部分的面积是多少?
的长为πcm,OD=3cm,求图中阴影部分的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的长为( )
A.![]()
B.![]()
C.4
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量校园内一棵不可攀的树的高度,数学应用实践小组做了如下的探索实践:根据《物理学》中光的反射定律,利用一面镜子和一根皮尺,设计如图的测量方案:把镜子放在离树(AB)9米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.7米,观察者目高CD=1.8米,则树(AB)的高度为米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.
(1)证明不论E、F在BC.CD上如何滑动,总有BE=CF;
(2)当点E、F在BC.CD上滑动时,分别探讨四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整,原题:如图1,在平行四边形ABCD中,点E是BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G. 若 ![]() , 求
, 求 ![]() 的值.
的值.
(1)尝试探究:
在图1中,过点E作EH∥AB交BG于点H,则AB和EH的数量关系是 ,
CG和EH的数量关系是 , ![]() 的值是 .
的值是 .
(2)类比延伸:如图2,在原题条件下,若 ![]() (m>0)则
(m>0)则 ![]() 的值是(用含有m的代数式表示),试写出解答过程 .
的值是(用含有m的代数式表示),试写出解答过程 .
(3)拓展迁移:如图3,梯形ABCD中,DC∥AB,点E是BC的延长线上的一点,AE和BD相交于点F,若 ![]() (a>0,b>0)则
(a>0,b>0)则 ![]() 的值是(用含a、b的代数式表示).
的值是(用含a、b的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com