
【题目】如图,在正△ABC中,D,E分别在AC,AB上,且 ![]() ,AE=BE,则有( )
,AE=BE,则有( )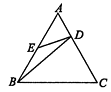
A.△AED∽△ABC
B.△ADB∽△BED
C.△BCD∽△ABC
D.△AED∽△CBD
科目:初中数学 来源: 题型:
【题目】如图,在扇形OAB中,∠AOB=90°,半径OA=2 ![]() ,将扇形OAB沿过点B的直线折叠,点O恰好落在
,将扇形OAB沿过点B的直线折叠,点O恰好落在 ![]() 上的点D处,折痕交OA于点C,则阴影部分的面积是 .
上的点D处,折痕交OA于点C,则阴影部分的面积是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=120°,S△ABC=8![]() ,点M,P,N分别是边AB,BC,AC上任意一点,则:
,点M,P,N分别是边AB,BC,AC上任意一点,则:
(1)AB的长为____________.
(2)PM+PN的最小值为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(列二元一次方程组解应用题)某公司共有3个一样规模的大餐厅和2个一样规模的小餐厅,经过测试同时开放2个大餐厅和1个小餐厅,可供300名员工就餐;同时开放1个大餐厅,1个小餐厅,可供170名员工就餐.
(1)请问1个大餐厅、1个小餐厅分别可供多少名员工就餐;
(2)如果3个大餐厅和2个小餐厅全部开放,那么能否供全体450名员工就餐?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 的对称轴为直线
的对称轴为直线 ![]() ,与
,与 ![]() 轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论: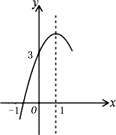
① ![]() ;② 方程
;② 方程 ![]() 的两个根是
的两个根是 ![]() ;③
;③ ![]() ;④当
;④当 ![]() 时,
时, ![]() 的取值范围是
的取值范围是 ![]() ;⑤ 当
;⑤ 当 ![]() 时,
时, ![]() 随
随 ![]() 增大而增大;其中结论正确有.
增大而增大;其中结论正确有.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在北京2008年第29届奥运会前夕,某超市在销售中发现:奥运会吉祥物— “福娃”平均每天可售出20套,每件盈利40元。为了迎接奥运会,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存。经市场调查发现:如果每套降价4元,那么平均每天就可多售出8套。要想平均每天在销售吉祥物上盈利1200元,那么每套应降价多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,求:
(1)边AC,AB,BC的长;
(2)点C到AB边的距离;
(3)求△ABC的面积.
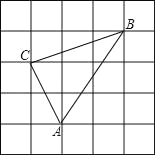
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3位置时,(2)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由.
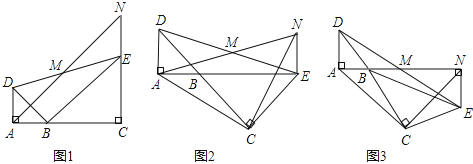
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com