
| A. | $\frac{1}{210}$ | B. | $\frac{1}{231}$ | C. | $\frac{1}{190}$ | D. | $\frac{1}{171}$ |
分析 根据$\frac{1}{1×20}$=$\frac{1}{21}$×($\frac{1}{1}$+$\frac{1}{20}$),这个规律转换题目,即可解决问题.
解答 解:原式=$\frac{2}{21}$×(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{20}$)-$\frac{2}{21}$(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{19}$)
=$\frac{2}{21}$×$\frac{1}{20}$
=$\frac{1}{210}$,
故选A.
点评 本题考查有理数的混合运算,解题的关键是利用规律转换题目,达到化简题目的目的,属于中考常考题型.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
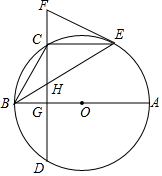 AB是⊙O的直径,点E是⊙O上一个点,C是弧BE的中点,弦CD⊥AB,G为垂足,且交BE于点H,经过点E作⊙O的切线交DC的延长线于点F.
AB是⊙O的直径,点E是⊙O上一个点,C是弧BE的中点,弦CD⊥AB,G为垂足,且交BE于点H,经过点E作⊙O的切线交DC的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
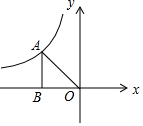 如图,点A在反比例函数y=$\frac{m-3}{x}$的图象上,连接OA,作AB⊥x轴,垂足为B,点A的坐标为(-2,n),OA=2$\sqrt{2}$.
如图,点A在反比例函数y=$\frac{m-3}{x}$的图象上,连接OA,作AB⊥x轴,垂足为B,点A的坐标为(-2,n),OA=2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com