
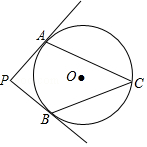
 如图,PA、PB分别切⊙O于点A、B,点C在⊙O上,且∠ACB=54°,则∠P=72°.
如图,PA、PB分别切⊙O于点A、B,点C在⊙O上,且∠ACB=54°,则∠P=72°.  寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:选择题
| A. | (-3,2) | B. | (3,2) | C. | (-3,-2) | D. | (3,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
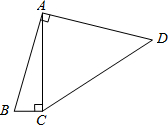 如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是什么?
如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是什么?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 顶点作标为(-3,2) | B. | 对称轴为:直线x=-3 | ||
| C. | 当x≥3时y随x增大而减小 | D. | 函数的最小值是2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{210}$ | B. | $\frac{1}{231}$ | C. | $\frac{1}{190}$ | D. | $\frac{1}{171}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
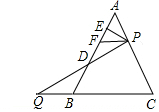 如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点.与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D,过P作PF∥BC.
如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点.与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D,过P作PF∥BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com