
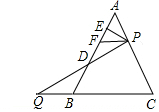
 ��ͼ����ABC�DZ߳�Ϊ6�ĵȱ������Σ�P��AC����һ���㣬��A��C�˶�����A��C���غϣ���Q��CB�ӳ�����һ���㣮���Pͬʱ����ͬ���ٶ���B��CB�ӳ��߷����˶���Q����B�غϣ�����P��PE��AB��E������PQ��AB��D����P��PF��BC��
��ͼ����ABC�DZ߳�Ϊ6�ĵȱ������Σ�P��AC����һ���㣬��A��C�˶�����A��C���غϣ���Q��CB�ӳ�����һ���㣮���Pͬʱ����ͬ���ٶ���B��CB�ӳ��߷����˶���Q����B�غϣ�����P��PE��AB��E������PQ��AB��D����P��PF��BC������ ��1����֤����AFP�ǵȱ������Σ���AP=PF=BQ����֤����BDQ�ա�FDP����BD=FD��
��2����P��Q���ٶ�Ϊv����AP=BQ=2v������ֱ�ǡ�QPC�У�30������Ե�ֱ�DZ���б�ߵ�һ����ʽ�ó����ۣ�
��3���������ߣ�����ƽ���ı���EQBP����֤����AEP�ա�BFQ����AE=BF��PE=FQ����һ��Ա�ƽ������ȵ��ı�����ƽ���ı��εó���?EQBP����Խ�����ƽ�֣�DE=DF=$\frac{1}{2}$EF����ΪEF=AB������DE=3������ı䣮
��� 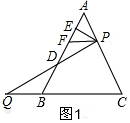 ֤������1����ͼ1��������ã�AP=BQ��
֤������1����ͼ1��������ã�AP=BQ��
�ߡ�ABCΪ�ȱ������Σ�
���ABC=��ACB=��A=60�㣬
��PF��BC��
���AFP=��ABC=60�㣬��APF=��C=60�㣬��FPD=��QBD��
���AFP�ǵȱ������Σ�
��PF=AP��
��PF=BQ��
�ߡ�FDP=��BDQ��
���BDQ�ա�FDP��
��BD=FD��
��2����ͼ1���ߡ�C=60�㣬��BQD=30�㣬
���QPC=90�㣬
��QC=2PC��
��P��Q���ٶ�Ϊv����AP=BQ=2v��
��PC=6-2v��QC=6+2v��
��6+2v=2��6-2v����
v=1��
��P��Q���ٶ�Ϊ1��
��3����ͼ2�����˶��������߶�ED�ij����ᷢ���仯�������ǣ�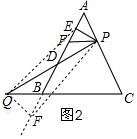
��QF��AB����AB���ӳ����ڵ�F������QE��PF��
��PE��AB��
���AEP=��QFB=90�㣬PE��FQ��
�ߡ�A=��ABC=��QBF=60�㣬AP=BQ��
���AEP�ա�BFQ��
��AE=BF��PE=FQ��
���ı���EQFP��ƽ���ı��Σ�
��DE=$\frac{1}{2}$EF��
��BE+AE=BE+BF=AB��
��DE=$\frac{1}{2}$AB��
�ߡ�ABC�DZ߳�Ϊ6�ĵȱ������Σ���AB=6��
��DE=3��
�����˶��������߶�ED�ij����ᷢ���仯��
���� �����������ε��ۺ��⣬�����˵ȱ������Ρ�ȫ�������Ρ�ֱ�������ε����ʣ���������ƽ���ı��ε����ʺ��ж�����1����2����Ϊ��������3�����Ѷȣ�ǡ���ع���ƽ���ı����ǹؼ���֤��������ȫ���ǵ�3�ʵ�ͻ�ƿڣ��ɶ�Ӧ����ȣ�����ƽ���ı��εĶԽ�����ƽ�ּ��߶εĺͽ��б��Σ�����ó����ۣ�


 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
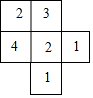 ��ͼ����һ����С�������ɵļ�����ĸ���ͼ��С�������е����ֱ�ʾ�ڸ�λ�õ�������ĸ��������㻭�������濴�ʹ����濴����ͼ�Σ�Ҫ��ֱ������
��ͼ����һ����С�������ɵļ�����ĸ���ͼ��С�������е����ֱ�ʾ�ڸ�λ�õ�������ĸ��������㻭�������濴�ʹ����濴����ͼ�Σ�Ҫ��ֱ�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
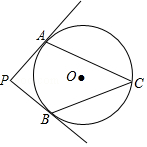 ��ͼ��PA��PB�ֱ��С�O�ڵ�A��B����C�ڡ�O�ϣ��ҡ�ACB=54�㣬���P=72�㣮
��ͼ��PA��PB�ֱ��С�O�ڵ�A��B����C�ڡ�O�ϣ��ҡ�ACB=54�㣬���P=72�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
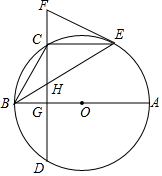 AB�ǡ�O��ֱ������E�ǡ�O��һ���㣬C�ǻ�BE���е㣬��CD��AB��GΪ���㣬�ҽ�BE�ڵ�H��������E����O�����߽�DC���ӳ����ڵ�F��
AB�ǡ�O��ֱ������E�ǡ�O��һ���㣬C�ǻ�BE���е㣬��CD��AB��GΪ���㣬�ҽ�BE�ڵ�H��������E����O�����߽�DC���ӳ����ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
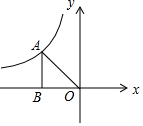 ��ͼ����A�ڷ���������y=$\frac{m-3}{x}$��ͼ���ϣ�����OA����AB��x�ᣬ����ΪB����A������Ϊ��-2��n����OA=2$\sqrt{2}$��
��ͼ����A�ڷ���������y=$\frac{m-3}{x}$��ͼ���ϣ�����OA����AB��x�ᣬ����ΪB����A������Ϊ��-2��n����OA=2$\sqrt{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com