

���� ��1����0��t��8��t��8������������ͼ�ν��
��2�����ô���ϵ�������ֱ��BC�Ľ���ʽ������AH��BC�������AH�Ľ���ʽ�����ɽ��⣻
��3����OQ��AH���������OQ=HQ��������á�OHP=45�㣻
��4����ֱ��DN����ʽΪy=kx+b������D������ֱ��DM��DN�Ľ���ʽ������S��BDM-S��ADN��ֵ���ɽ���
��� �⣺��1���ߵ�B������Ϊ��0��-4����
��OB=4��
��0��t��8ʱ��OP=4-0.5t��
��t��8ʱ��OP=4+0.5t��
��2����ֱ��BC�Ľ���ʽΪ��y=kx+b��
��$\left\{\begin{array}{l}{-k+b=0}\\{b=-4}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-4}\\{b=-4}\end{array}\right.$��
��ֱ��BC����ʽΪy=-4x-4��
��AH��BC��
����ֱ��AH����ʽΪy=$\frac{1}{4}$x+b��
�ѵ�A��4��0������AH����ʽ����b=-1��
��AH����ʽΪy=$\frac{1}{4}$x-1��
��x=0ʱ��y=-1��
��BP=OB-OP=3��
t=3��0.5=6��
��AH��BCʱ��t=6�룻
��3����OQ��AH��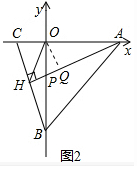
��OQ��AH����ֱ��OQ��O�㣬
��OQ����ʽΪy=-4x��
��ֱ��AH����ʽΪy=$\frac{1}{4}$x-1��ֱ��BC����ʽΪy=-4x-4��
��Q������x��-4x������-4x=$\frac{1}{4}$x-1��
��ã�x=$\frac{4}{17}$�ཻ��Q����Ϊ��$\frac{4}{17}$��-$\frac{16}{17}$����
��H������x��$\frac{1}{4}$x-1������$\frac{1}{4}$x-1=-4x-4��
��ã�x=-$\frac{12}{17}$��
���H������-$\frac{12}{17}$��-$\frac{20}{17}$����
��QH=OQ��
���OHP=45�㣻
��3��D��ΪAB�е㣬��D��2��-2����
��ֱ��DN����ʽΪy=kx+b������D���b=-2-2k��
��ֱ��DN����ʽΪy=kx-2-2k��
��ֱ��DP��DN������D��ã�ֱ��DP����ʽΪy=-$\frac{1}{k}$x+$\frac{2}{k}$-2��
��P�㣨0��$\frac{2}{k}$-2����N��$\frac{2}{k}$+2��0����
��S��BDP-S��ADN=$\frac{1}{2}$��2��$\frac{2}{k}$-2+4��-$\frac{1}{2}$��2��$\frac{2}{k}$+2-4����
=$\frac{2}{k}$+2+2-$\frac{2}{k}$=4��
���� ���⿼����ƽ��ֱ������ϵ���߶γ��ȵ���⣬������һ�κ�����ƽ��ֱ������ϵ�е����ã������и���һ�κ������������ǽ���Ĺؼ���


 ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
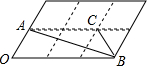 ��ͼ��6����״����С��ȫ��ͬ����������������εĶ����Ϊ��㣮��֪���ε�һ���ǣ���O��Ϊ60�㣬A��B��C���ڸ���ϣ���tan��ABC��ֵ�ǣ�������
��ͼ��6����״����С��ȫ��ͬ����������������εĶ����Ϊ��㣮��֪���ε�һ���ǣ���O��Ϊ60�㣬A��B��C���ڸ���ϣ���tan��ABC��ֵ�ǣ�������| A�� | $\frac{\sqrt{3}}{2}$ | B�� | $\frac{\sqrt{3}}{3}$ | C�� | $\sqrt{3}$ | D�� | $\frac{2\sqrt{3}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
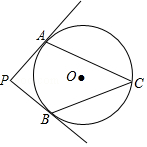 ��ͼ��PA��PB�ֱ��С�O�ڵ�A��B����C�ڡ�O�ϣ��ҡ�ACB=54�㣬���P=72�㣮
��ͼ��PA��PB�ֱ��С�O�ڵ�A��B����C�ڡ�O�ϣ��ҡ�ACB=54�㣬���P=72�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
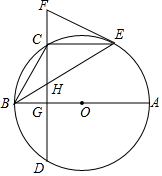 AB�ǡ�O��ֱ������E�ǡ�O��һ���㣬C�ǻ�BE���е㣬��CD��AB��GΪ���㣬�ҽ�BE�ڵ�H��������E����O�����߽�DC���ӳ����ڵ�F��
AB�ǡ�O��ֱ������E�ǡ�O��һ���㣬C�ǻ�BE���е㣬��CD��AB��GΪ���㣬�ҽ�BE�ڵ�H��������E����O�����߽�DC���ӳ����ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com