
��ͼ���ھ���ABCD�У�AB=6�ף�BC=8�ף�����P��2��/����ٶȴӵ�A��������AC���C�ƶ���ͬʱ����Q��1��/����ٶȴӵ�C��������CB���B�ƶ�����P��Q�����ƶ�t�루0��t��5����������CPQ�����ΪS��2��
��1�������S��ʱ��t�Ĺ�ϵʽ��
��2����P��Q�����ƶ��Ĺ����У��ı���ABQP���CPQ������ܷ���ȣ����ܣ������ʱ��P��λ�ã������ܣ���˵�����ɣ�
��3��tΪ��ֵʱ��������CPQΪֱ�������Σ�

�����㡿�ı����ۺ��⣮
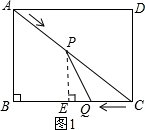
����������1������P��PE��BC��E�����ù��ɶ������AC�ij���AP=2t��CQ=t����PC=10﹣2t����PE��AB������ƽ���߷��߶γɱ����г�����ʽ���ɵó�PE�ij������������ε������ʽ���ɵó����ۣ�
��2�������ı���ABQP���CPQ�������ȣ���S��PCQ=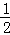 S��ABC�����жϳ����̸���������ɣ�
S��ABC�����жϳ����̸���������ɣ�
��3���֡�PQC=90�����CPQ=90����������������ۼ��ɣ�
����𡿽⣺��1����ͼ1������P��PE��BC��E��Rt��ABC�У�AC=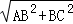 =
=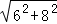 =10��m����
=10��m����
������֪��AP=2t��CQ=t����PC=10﹣2t��
��AB��BC��PE��BC����PE��AB��
��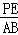 =
=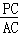 ����
����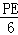 =
=
��PE=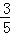 ��10﹣2t��=﹣
��10﹣2t��=﹣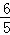 t+6��
t+6��
��S��PCQ=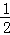 CQ•PE=
CQ•PE=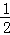 t•��﹣
t•��﹣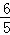 t+6��=﹣
t+6��=﹣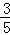 t2+3t��0��t��5����
t2+3t��0��t��5����
��2�����ܣ�
���ɣ������ı���ABQP���CPQ�������ȣ�
��S��PCQ=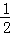 S��ABC����﹣
S��ABC����﹣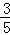 t2+3t=
t2+3t=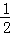 ��6��8�������ã�t2﹣5t+40=0��
��6��8�������ã�t2﹣5t+40=0��
�ߡ�=��﹣5��2﹣160=﹣135��0��
��t�⣬
�����ABQP���CPQ�����������ȣ�
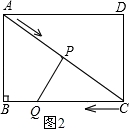
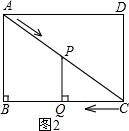
��3����ͼ2������PQC=90��ʱ��PQ��BC��
��AB��BC��AB=6��BC=8��QC=t��PC=10﹣2t��
���PQC�ס�ABC��
��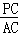 =
=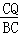 ����
����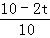 =
=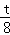 �����t=
�����t=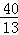 ���룩��
���룩��
��ͼ3������CPQ=90��ʱ��PQ��AC��
�ߡ�ACB=��QCP����B=��QPC��
���CPQ�ס�CBA��
��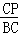 =
=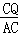 ����
����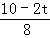 =
=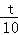 �����t=
�����t=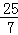 ���룩��
���룩��
����������tΪ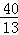 ����
����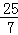 ��ʱ����CPQΪֱ�������Σ�
��ʱ����CPQΪֱ�������Σ�
�����������⿼������ı����ۺ��⣬�漰�����ε����ʡ����ɶ����������б�ʽ�������ε������ʽ��ƽ���߷��߶γɱ�����֪ʶ������ؼ��Ƕ���Щ֪ʶ���������ռ�������ã��ڽ��3��ʱҪע��������ۣ�


 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
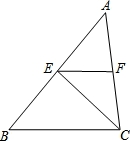
��ͼ���ڡ�ABC�У�E��F�ֱ���AB��AC���е㣬��CEF�����Ϊ2.5�����ABC�����Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�Ķ����в��ϣ�
������ȫƽ����ʽ�����Խ�����ʽ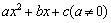 ����Ϊ
����Ϊ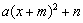 ����ʽ, ���ǰ������ı��η�����������ʽ
����ʽ, ���ǰ������ı��η�����������ʽ ���䷽����
���䷽����
���ö���ʽ���䷽����ƽ���ʽ�ܶ�һЩ����ʽ���зֽ���ʽ��
���磺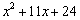 ��
��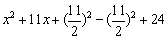
��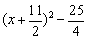
��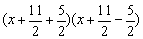
��
�������ϲ��ϣ�����������⣺
��1���ö���ʽ���䷽����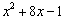 ����
����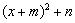 ����ʽ��
����ʽ��
��2��������ijλͬѧ���䷽����ƽ���ʽ�Ѷ���ʽ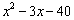 ���зֽ���ʽ�Ľ����̣�
���зֽ���ʽ�Ľ����̣�
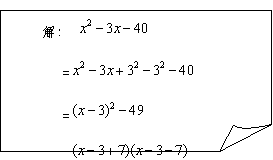 |
��ʦ˵����λͬѧ�Ľ��������д��������ҳ���ͬѧ����п�ʼ���ִ���ĵط������á� ���껭������Ȼ��д�������ġ���ȷ�Ľ����̣�
��3����֤��x��yȡ�κ�ʵ��ʱ������ʽ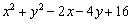 ��ֵ��Ϊ������
��ֵ��Ϊ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
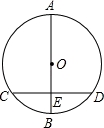
��ͼ����Oֱ��AB��ֱ����CD������E��OB���е㣬CD=6cm����ֱ��AB=__________cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
һ�������IJ�����װ�к졢�ơ���������ɫ������ɫ��ͬ�����������κ����𣩣����к���2��������1��������1����
��1����Ӵ�����������һ�����Ǻ���ĸ��ʣ�
��2����һ�δӴ�����������һ��������ɫ��Żش��У��ڶ���������һ���������ɫ�����û���״ͼ���б��ķ��������ζ���������ĸ��ʣ���������ֱ������1����2����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
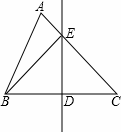
��ͼ����ABC�У�AB=8��AC=11��BC���ϵĴ�ֱƽ���߷ֱ�AC��BC�ڵ�E��D�����ABE���ܳ����� .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
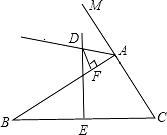
���棺��ͼ����ABC�ı�BC�Ĵ�ֱƽ����DE����BAC�����ƽ����AD��D��EΪ���㣬DF��AB��F����AB��AC����֤��BF=AC+AF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����ƽ��ֱ������ϵ�У�ֱ��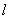 ��x�ᣬ��ֱ��
��x�ᣬ��ֱ��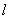 �ֱ��뷴��������y=
�ֱ��뷴��������y=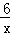 ��x��0����y=��
��x��0����y=��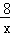 ��x��0����ͼ���ڵ�P��Q������PO��QO�����POQ�����Ϊ .
��x��0����ͼ���ڵ�P��Q������PO��QO�����POQ�����Ϊ .
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com