练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    阅读下列材料：

    利用完全平方公式，可以将多项式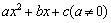变形为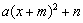的形式, 我们把这样的变形方法叫做多项式的配方法．

    运用多项式的配方法及平方差公式能对一些多项式进行分解因式．

    例如：＝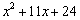

    ＝

    ＝

    ＝

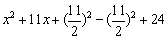
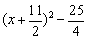
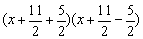
    根据以上材料，解答下列问题：

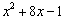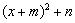    （1）用多项式的配方法将化成的形式；

    （2）下面是某位同学用配方法及平方差公式把多项式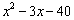进行分解因式的解答过程：

     


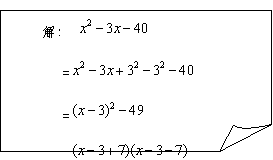    老师说，这位同学的解答过程中有错误，请你找出该同学解答中开始出现错误的地方，并用“      ”标画出来，然后写出完整的、正确的解答过程：

    （3）求证：x，y取任何实数时，多项式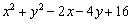的值总为正数．



    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


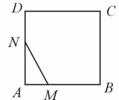
    如图，在正方形ABCD中，AB=3cm，动点M自A点出发沿AB方向以每秒1cm的速度运动，同时动点N自A点出发沿折线AD—DC—CB以每秒3cm的速度运动，到达B点时运动同时停止，设△AMN的面积为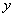（cm2），运动时间为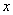（秒），则下列图象中能大致反映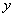与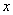之间的函数关系的是

     


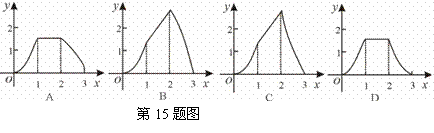    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图1，已知二次函数y=ax2﹣8ax+12（a＞0）的图象与x轴分别交于A、B两点，与y轴交于点C，点P在抛物线的对称轴上，且四边形ABPC为平行四边形．

    （1）求此抛物线的对称轴，并确定此二次函数的解析式；

    （2）点M为x轴下方抛物线上一点，若△OMP的面积为36，求点M的坐标．

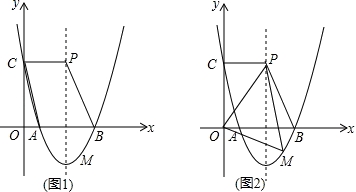
    查看答案和解析>>

    科目：初中数学 来源： 题型：


    对于一次函数，当-2≤≤3时，函数值的取值范围 是                  ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若=，则的值为(     )

    A．      B．      C．      D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    抛物线y=（x﹣3）2+5的顶点坐标是__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在矩形ABCD中，AB=6米，BC=8米，动点P以2米/秒的速度从点A出发，沿AC向点C移动，同时动点Q以1米/秒的速度从点C出发，沿CB项点B移动，设P、Q两点移动t秒（0＜t＜5）后，三角形CPQ的面积为S米2．

    （1）求面积S与时间t的关系式；

    （2）在P、Q两点移动的过程中，四边形ABQP与△CPQ的面积能否相等？若能，求出此时点P的位置；若不能，请说明理由．

    （3）t为何值时，三角形CPQ为直角三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如果点(a，b)在第二象限，那么(a，b)在第     象限．

    查看答案和解析>>

    同步练习册答案