
【题目】如图,等边△ABC中, AO是∠BAC的角平分线, D为 AO上一点,以 CD为一边且在 CD下方作等边△CDE,连接BE.
(1)求证:△ACD≌△BCE.
(2)延长BE至Q, P为BQ上一点,连接 CP、CQ使 CP=CQ=5,若 BC=6,求PQ的长.

【答案】(1)详见解析;(2)PQ=8.
【解析】
(1)根据等边三角形得∠ACD=∠BCE,即可证明△ACD≌△BCE(SAS),
(2)过C作CH⊥BQ ,垂足为 H,由角平分线得到∠CAD= ![]() ∠BAC=30°,通过(1)得∠CAD=∠CBH=30°,根据30°角所对直角边等于斜边一半求出CH=3,勾股定理得HQ=4,三线合一性质即可求出PQ=8.
∠BAC=30°,通过(1)得∠CAD=∠CBH=30°,根据30°角所对直角边等于斜边一半求出CH=3,勾股定理得HQ=4,三线合一性质即可求出PQ=8.
(1)证明:∵△ABC, △CDE 均为等边三角形,
∴∠ACB=∠DCE=60°,
∴∠ACB-∠DCO=∠DCE-∠DCO,即∠ACD=∠BCE ,
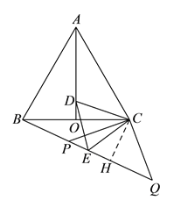
在△ACD 和△BCE 中,
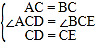 ,
,
∴△ACD≌△BCE(SAS)
(2)解:∵等边△ABC中,AO平分∠BAC,∴∠CAD= ![]() ∠BAC=30°.
∠BAC=30°.
如下图,过C点作CH⊥BQ ,垂足为 H,
由(1)知△ACD≌△BCE ,
则∠CAD=∠CBH=30°,
∴CH=![]() BC=3 ,
BC=3 ,
∴在Rt△CHQ 中,HQ=4(勾股定理) ,
又∵CP=CQ,CH⊥PQ,
∴PH=HQ(三线合一)
∴ PQ=8.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,点E、F、G. H分别AB、BC、 CD、 DA边上的动点,且AE=BF=CG=DH

(1)求证:四边形EFGH是平行四边形:
(2)在点E、F、G、H运动过程中,判断直线GE是否经过某一定点,如果是,请你在图中画出这个点:如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图像经过点(0,3)、(3,0)和(1,4).
(1)求该二次函数的表达式;
(2)若该二次函数图像的顶点为P,与x轴分别交于点A、B,求△ABP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
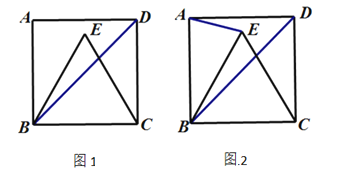
【题目】在正方形ABCD中,E是△ABD内的点,EB=EC.
(1)如图1,若EB=BC,求∠EBD的度数;
(2)如图2,EC与BD交于点F,连接AE,若![]() ,试探究线段FC与BE之间的等量关系,并说明理由.
,试探究线段FC与BE之间的等量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对称轴为直线x=1的抛物线y=ax2+bx+8过点(﹣2,0).
(1)求抛物线的表达式,并写出其顶点坐标;
(2)现将此抛物线沿y轴方向平移若干个单位,所得抛物线的顶点为D,与y轴的交点为B,与x轴负半轴交于点A,过B作x轴的平行线交所得抛物线于点C,若AC∥BD,试求平移后所得抛物线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,坡AB的坡比为1:2.4,坡长AB=130米,坡AB的高为BT.在坡AB的正面有一栋建筑物CH,点H、A、T在同一条地平线MN上.

(1)试问坡AB的高BT为多少米?
(2)若某人在坡AB的坡脚A处和中点D处,观测到建筑物顶部C处的仰角分别为60°和30°,试求建筑物的高度CH.(精确到米, ![]() ≈1.73,
≈1.73, ![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图a是一个长为2m、宽为2n的长方形,沿图中实现用剪刀均分成四块小长方形,然后按图b的形状拼成一个正方形.
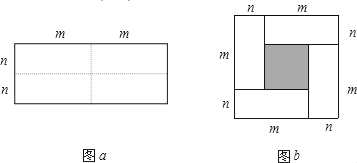
(1)图b中,大正方形的边长是 .阴影部分小正方形的边长是 ;
(2)观察图b,写出(m+n)2,(m﹣n)2,mn之间的一个等量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
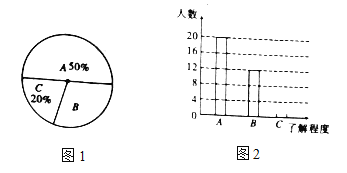
【题目】为传播奥运知识,小刚就本班学生对奥运知识的了解程度进行了一次调查统计:A:熟悉,B:了解较多,C:一般了解图1和图2是他采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
(1)求该班共有多少名学生;
(2)在条形图中,将表示“一般了解”的部分补充完整;
(3)在扇形统计图中,计算出“了解较多”部分所对应的圆心角的度数;
(4)如果全年级共1000名同学,请你估算全年级对奥运知识“了解较多”的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com