
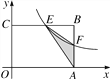
【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=![]() (x>0)的图象与BC边交于点E.
(x>0)的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?
【答案】(1)y=![]() (x>0)(2)当k=3时,S△EFA有最大值,最大值为
(x>0)(2)当k=3时,S△EFA有最大值,最大值为![]() .
.
【解析】试题分析:(1)、首先得出点B的坐标,然后根据中点得出点F的坐标,最后利用待定系数法求出函数解析式;(2)、首先得出点E和点F的坐标,然后根据三角形的面积计算法则得出关于k的二次函数,然后根据函数的增减性得出最大值.
试题解析:(1)∵在矩形OABC中,OA=3,OC=2, ∴B(3,2),∵F为AB的中点,
∴F(3,1), ∵点F在反比例函数y=![]() (k>0)的图象上, ∴k=3,
(k>0)的图象上, ∴k=3,
∴该函数的解析式为y=![]() (x>0);
(x>0);
(2)由题意知E,F两点坐标分别为E(![]() ,2),F(3,
,2),F(3,![]() ),
),
∴S△EFA=![]() AFBE=
AFBE=![]() ×
×![]() k(3﹣
k(3﹣![]() k)=
k)=![]() k﹣
k﹣![]() k2=﹣
k2=﹣![]() (k2﹣6k+9﹣9)=﹣
(k2﹣6k+9﹣9)=﹣![]() (k﹣3)2+
(k﹣3)2+![]()
当k=3时,S有最大值.
S最大值=![]() .
.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
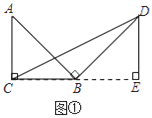
【题目】问题原型:如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.过点D作△BCD的BC边上的高DE, 易证△ABC≌△BDE,从而得到△BCD的面积为![]() .
.
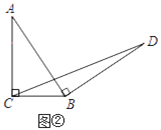
初步探究:如图②,在Rt△ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.用含a的代数式表示△BCD的面积,并说明理由.
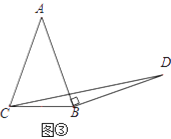
简单应用:如图③,在等腰三角形ABC中,AB=AC,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.直接写出△BCD的面积.(用含a的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某专卖店专营某品牌的衬衫,店主对上一周中不同尺码的衬衫销售情况统计如下:
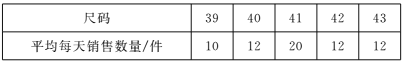
该店主决定本周进货时,增加一些41码的衬衫,影响该店主决策的统计量是( )
A.平均数 B.方差 C.众数 D.中位数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△![]() C;平移△ABC,若A的对应点
C;平移△ABC,若A的对应点![]() 的坐标为(0,4),画出平移后对应的△
的坐标为(0,4),画出平移后对应的△![]() ;
;
(2)若将△![]() C绕某一点旋转可以得到△
C绕某一点旋转可以得到△![]() ,请直接写出旋转中心的坐标;
,请直接写出旋转中心的坐标;
(3)在![]() 轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料,回答问题:
解方程x4-5x2+4=0,这是一个一元四次方程,根据该方程的特点,它的解法通常是:
设x2=y,那么x4=y2,于是原方程可变为y2-5y+4=0 ①,解得y1=1,y2=4.
当y=1时,x2=1,∴x=±1;当y=4时,x2=4,∴x=±2;
∴原方程有四个根:x1=1,x2=-1,x3=2,x4=-2.
(1)在由原方程得到方程①的过程中,利用 法(把未知数x换为 y)达到降次的目的.
(2)解方程:(x2+3x)2+5(x2+3x)-6=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
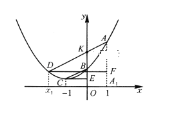
【题目】如图,已知点A(1,yA),B(0,yB),C(-1,yC),D(x1,yD)(x1≠1)在抛物线![]() 上,且AD//BC,AA1
上,且AD//BC,AA1![]() 轴于A1,DF⊥AAl于F,CE⊥
轴于A1,DF⊥AAl于F,CE⊥![]() 轴于E.
轴于E.
(1)求证:△ADF∽△BCE;
(2)当![]() ,
,![]() ,
,![]() 时,求
时,求![]() 的值;
的值;
(3)![]() 的值会随a,b,c的值改变而改变吗?若会,请求出
的值会随a,b,c的值改变而改变吗?若会,请求出![]() 与a,b,c的关系式;若不会,请说明理由.
与a,b,c的关系式;若不会,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=-1,有以下结论:①abc>0;②4ac<b2;③2a+b=0;④a-b+c>0.其中正确的结论的个数是( )
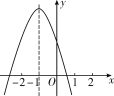
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于频率与概率有下列几种说法:①“明天下雨的概率是90%”表示明天下雨的可能性很大;②“抛一枚硬币正面朝上的概率为![]() ”表示每抛两次就有一次正面朝上;③“某彩票中奖的概率是1%”表示买10张该种彩票不可能中奖;④“抛一枚硬币正面朝上的概率为
”表示每抛两次就有一次正面朝上;③“某彩票中奖的概率是1%”表示买10张该种彩票不可能中奖;④“抛一枚硬币正面朝上的概率为![]() ”表示随着抛掷次数的增加,“抛出正面朝上”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出正面朝上”这一事件发生的频率稳定在![]() 附近,正确的说法是( )
附近,正确的说法是( )
A. ②④B. ②③C. ①④D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商场销售一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下.若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?
(2)每千克水果涨价多少元时,商场每天获得的利润最大?获得的最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com