
����Ŀ������ԭ�ͣ���ͼ�����ڵ���ֱ��������ABC�У���ACB=90����BC=a������AB�Ƶ�B˳ʱ����ת90���õ��߶�BD������CD������D����BCD��BC���ϵĸ�DE�� ��֤��ABC�ա�BDE���Ӷ��õ���BCD�����Ϊ![]() ��
��
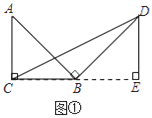
����̽������ͼ������Rt��ABC�У���ACB=90����BC=a������AB�Ƶ�B˳ʱ����ת90���õ��߶�BD������CD���ú�a�Ĵ���ʽ��ʾ��BCD���������˵�����ɣ�
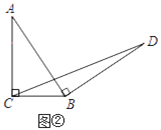
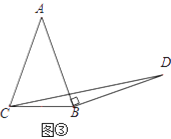
��Ӧ�ã���ͼ�����ڵ���������ABC�У�AB=AC��BC=a������AB�Ƶ�B˳ʱ����ת90���õ��߶�BD������CD��ֱ��д����BCD����������ú�a�Ĵ���ʽ��ʾ��
���𰸡�������
���������������:(1)����̽��:��ͼ��,����D��BC�Ĵ���,��BC���ӳ��߽��ڵ�E,�ɴ�ֱ�����ʾͿ��Եó���ABC�ա�BDE,����DE=BC=a,�����������ε������ʽ�ó�����,
(2)������:��ͼ��,����A��AF��BC��F,����D��DE��BC���ӳ����ڵ�E,�ɵ��������ε����ʿ��Եó�BF=![]() BC,���������Եó���AFB�ա�BED�Ϳ��Եó�BF=DE,�������ε������ʽ�Ϳ��Եó�����.
BC,���������Եó���AFB�ա�BED�Ϳ��Եó�BF=DE,�������ε������ʽ�Ϳ��Եó�����.
�������:(1)��BCD�����Ϊ![]() ,
,
����:��ͼ��,����D��BC�Ĵ���,��BC���ӳ��߽��ڵ�E,
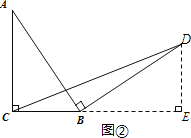
���BED=��ACB=90��,
���߶�AB�Ƶ�B˳ʱ����ת90���õ��߶�BE,
��AB=BD,��ABD=90��,
���ABC+��DBE=90��,
�ߡ�A+��ABC=90��,
���A=��DBE,
�ڡ�ABC�͡�BDE��,
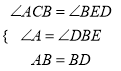 ,
,
���ABC�ա�BDE��AAS��,
��BC=DE=a,
��S��BCD= ![]()
��S��BCD=![]() ,
,
(2)��Ӧ��:��ͼ��,����A��AF��BC��F,����D��DE��BC���ӳ����ڵ�E,
���AFB=��E=90��,BF= ![]() ,
,
���FAB+��ABF=90��,
�ߡ�ABD=90��,
���ABF+��DBE=90��,
���FAB=��EBD,
���߶�BD�����߶�AB��ת�õ���,
��AB=BD,
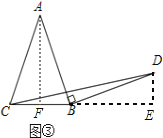
�ڡ�AFB�͡�BED��,
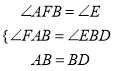 ,
,
���AFB�ա�BED��AAS��,
��BF=DE= ![]() ,
,
��S��BCD= ![]() ,
,
��S��BCD=![]() ,
,
���BCD�����Ϊ![]() ,
,



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ABC��90�㣬AB��8cm��BC��6cm������P��Q�ֱ�ӵ�A��Bͬʱ��ʼ�ƶ�����P���ٶ�Ϊ1 cm���룬��Q���ٶ�Ϊ2 cm���룬��Q�ƶ�����C��ֹͣ����PҲ��ֹ֮ͣ�˶�����ʱ��˲���У���ʹ��PBQ�����Ϊ15cm ���ǣ� ��
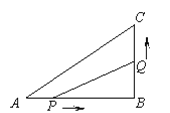
A. 2���� B. 3���� C. 4���� D. 5����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��ͼ��ֱ��㣨0��3����3��0������2����5����
��1����������κ����Ľ���ʽ��
��2����������κ�����ͼ����x�ύ�ڵ�C��D��C���ڵ�D����ࣩ���ҵ�A�Ǹ�ͼ��Ķ��㣬����������κ����ĶԳ�����ȷ��һ��B��ʹ��ABC�ǵ��������Σ������B�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ��� Rt��ABC �У�AC��BC�� 2![]() ���� P ����б�� AB Ϊֱ���İ�Բ�ϣ�M Ϊ PC���е㣮���� P �ذ�Բ�ӵ� A �˶����� B ʱ���� M �˶���·�����ǣ� ��
���� P ����б�� AB Ϊֱ���İ�Բ�ϣ�M Ϊ PC���е㣮���� P �ذ�Բ�ӵ� A �˶����� B ʱ���� M �˶���·�����ǣ� ��
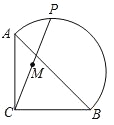
A. 2 B. 2 ![]() C. �� D.
C. �� D. ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
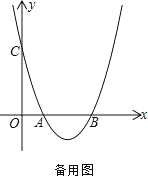
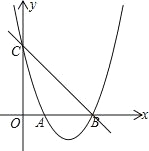
����Ŀ�������� y��ax2��bx��3 ������(2����1)���� x �ύ�� A(1��0)��B �������� y�ύ�ڵ� C
(1) �������߽���ʽ
(2) ��ͼ���� E ��ֱ�� BC �·��������ϵ�һ���㣮����BEC ������ʱ��������� E ������
(3) �� P �ǵ����������������ϵ�һ������PA �� y ���� D��BP �� y ���� E���� P �� PN��y ����N����![]() ��ֵ
��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������һ��ţ�̣�����Ϊÿ��24Ԫ���涨�ۼ۲����ڽ��ۣ����ڵ��ۼ�Ϊÿ��36Ԫ��ÿ�¿�����60�䣮�г����鷢�֣�������ţ�̵��ۼ�ÿ����1Ԫ����ÿ�µ�����������10�䣬��ÿ��ţ�̽���xԪ(xΪ������)��ÿ�µ�����Ϊy�䣮
��1��д��y��x�м�ĺ�����ϵʽ���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2��������ζ��ۣ�����ʹÿ������ţ�̵����������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������ͬһ�������������ľ���ʱ���֣�����ƽ��ֱ������ϵ����������P1��x1��y1����P2��x2��y2������ͨ������ֱ�����������ù��ɶ����õ����ۣ�P1P2=![]() ������֤�����߶�P1P2���е�P��x��y�������깫ʽ�ǣ�x=
������֤�����߶�P1P2���е�P��x��y�������깫ʽ�ǣ�x=![]() ��y=
��y=![]() ��
��
����Ӧ��
�������������Ϣ�������������⣺
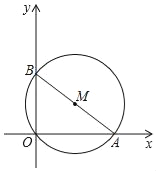
��ͼ����ƽ��ֱ������ϵ�У���֪A��8��0����B��0��6����C��1��7������M����ԭ��O����A��B��
��1�����M�İ뾶��Բ��M�����ꣻ
��2���жϵ�C���M��λ�ù�ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
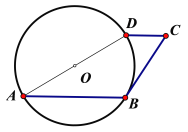
����Ŀ����ͼ����O��ֱ��AD��Ϊ6��AB���ң�CD��AB����A=30�㣬��CD=![]() ��
��
��1�����C�Ķ�����
��2����֤��BC�ǡ�O�����ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
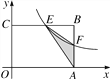
����Ŀ����ͼ���ھ���OABC�У�OA��3��OC��2��F��AB�ϵ�һ������(F����A��B�غ�)������F�ķ���������y��![]() (x��0)��ͼ����BC�߽��ڵ�E.
(x��0)��ͼ����BC�߽��ڵ�E.
(1)��FΪAB���е�ʱ����ú����Ľ���ʽ��
(2)��kΪ��ֵʱ����EFA���������������Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com