
【题目】已知二次函数y=ax2+bx+c的图象分别经过点(0,3)(3,0)(﹣2,﹣5),
(1)求这个二次函数的解析式;
(2)若这个二次函数的图象与x轴交于点C、D(C点在点D的左侧),且点A是该图象的顶点,请在这个二次函数的对称轴上确定一点B,使△ABC是等腰三角形,求出点B的坐标.
【答案】(1) 二次函数的解析式为y=﹣x2+2x+3;(2)① AC边为腰,AC=AB,则B(1,4﹣2![]() )或(1,4+2
)或(1,4+2![]() );②AC边为腰,AC=BC,则B(1,﹣4);③AC边为底,AB=BC,则B(1,
);②AC边为腰,AC=BC,则B(1,﹣4);③AC边为底,AB=BC,则B(1,![]() )
)
【解析】
(1)将![]() 三点坐标代入y=ax2+bx+c求解即可.
三点坐标代入y=ax2+bx+c求解即可.
(2)由解析式求出A、C两点坐标,再设出对称轴上的B点坐标,由三点确定一个等腰三角形求出B点坐标.
(1)将![]() 三点坐标代入y=ax2+bx+c,得:
三点坐标代入y=ax2+bx+c,得:
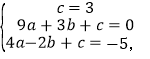
解得: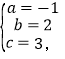
∴这个二次函数的解析式为![]()
(2)由y=﹣x2+2x+3可知,C(﹣1,0),A(1,4),由于B点在对称轴上,则设B点坐标为(1,y).
由于△ABC是等腰三角形,则分三种情况:
AC边为腰,AC=AB,则B(1,4﹣2![]() )或(1,4+2
)或(1,4+2![]() );
);
②AC边为腰,AC=BC,则B(1,﹣4);
③AC边为底,AB=BC,则B(1,![]() ).
).


科目:初中数学 来源: 题型:
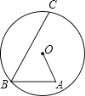
【题目】如图,在O内有折线OABC,点B、C在圆上,点A在O内,其中OA=4cm,BC=14cm,∠A=∠B=![]() ,则AB的长为__________________
,则AB的长为__________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于D.
(1)求证:△ADC∽△CDB;
(2)若AC=2,AB=![]() CD,求⊙O半径.
CD,求⊙O半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
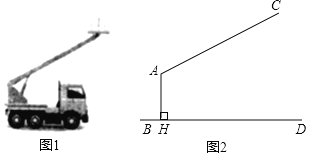
【题目】图1是一辆吊车的实物图,图2是其工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH为3.4m.当起重臂AC长度为9m,张角∠HAC为118°时,求操作平台C离地面的高度(结果保留小数点后一位:参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
查看答案和解析>>
科目:初中数学 来源: 题型:
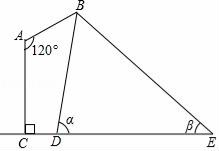
【题目】如图是某路灯在铅垂面内的示意图,灯柱AC的高为11米,灯杆AB与灯柱AC的夹角∠A=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为18米,从D,E两处测得路灯B的仰角分别为α和β,且tanα=6,tanβ=![]() ,求灯杆AB的长度.
,求灯杆AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
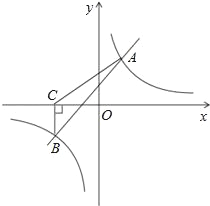
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象相交于A(2,3),B(﹣3,n)两点.
的图象相交于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b>![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
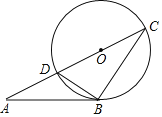
【题目】如图,DC是⊙O的直径,点B在圆上,直线AB交CD延长线于点A,且∠ABD=∠C.
(1)求证:AB是⊙O的切线;
(2)若AB=4cm,AD=2cm,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
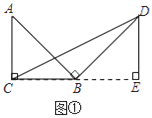
【题目】问题原型:如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.过点D作△BCD的BC边上的高DE, 易证△ABC≌△BDE,从而得到△BCD的面积为![]() .
.
初步探究:如图②,在Rt△ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.用含a的代数式表示△BCD的面积,并说明理由.
简单应用:如图③,在等腰三角形ABC中,AB=AC,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.直接写出△BCD的面积.(用含a的代数式表示)
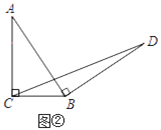
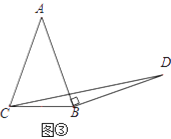
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某专卖店专营某品牌的衬衫,店主对上一周中不同尺码的衬衫销售情况统计如下:
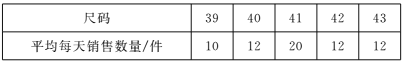
该店主决定本周进货时,增加一些41码的衬衫,影响该店主决策的统计量是( )
A.平均数 B.方差 C.众数 D.中位数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com