
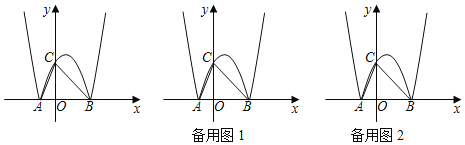
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y��x2��2x��3��x����A��B���㣨��A�ڵ�B����ࣩ������������λ��x���Ϸ���������M������������λ��x���·��IJ�����x�ᷭ�ۣ����ۺ�����������N������N��y���ڵ�C������AC��BC��
��1��������N���������ߵĺ�������ʽ��
��2�����ABC���Բ�������
��3����PΪ����M������N�ϵĶ��㣬��QΪx���ϵ�һ�����㣬���Ե�B��C��P��QΪ������ı�����ƽ���ı��Σ���ֱ��д����Q�����ꣻ
��4����ֱ��BC�Ϸ�������M��ȷ��������D1��D2��ʹ��![]() ��
��![]() ��S��ABC���������D1��D2�����ꣻ������M��N���Ƿ���������T1��T2��T3��T4��T5��ʹ���������ֱ����B��CΧ�ɵ������ε����Ϊ
��S��ABC���������D1��D2�����ꣻ������M��N���Ƿ���������T1��T2��T3��T4��T5��ʹ���������ֱ����B��CΧ�ɵ������ε����Ϊ![]() �������ڣ�ֱ��д���������T1��T2��T3��T4��T5�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ�ֱ��д���������T1��T2��T3��T4��T5�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y����x2+2x+3����2��5������3��Q��1��0����Q��2��![]() ��0����Q��2+
��0����Q��2+![]() ��0��ʱ�Ե�B��C��P��QΪ������ı�����ƽ���ı��Σ���4�����ڣ�T1����
��0��ʱ�Ե�B��C��P��QΪ������ı�����ƽ���ı��Σ���4�����ڣ�T1����![]() ��
��![]() ����T2��
����T2��![]() ��
��![]() ����T3��
����T3��![]() ��
��![]() ����T4��
����T4��![]() ��
��![]() ����T5��
����T5��![]() ��
��![]() ����
����
��������
��1����N��Mͼ���·��IJ��ֹ���x��Գƣ������N�Ľ���ʽ��
��2�����A��B��C�����꣬�ֱ���BC��AB�Ĵ�ֱƽ���߽��ڵ�O'����O'Ϊ��ABC�����Բ���ɵ��������ε����ʺ��ɶ����������Բ�뾶��
��3���������������P����M��ʱ����P��m��m2��2m��3����Q��n��0������P����N��ʱ����P��m����m2+2m+3����Q��n��0��������ÿ������з������������BQ��PC��BQ��PCʱ������BP��CQ��BP��CQʱ������ƽ���ı��ζԽ�����ƽ�ֵ����ʣ��е��غ�������������⣻
��4������֪�ɵ�D1D2����ֱ����ֱ��BCƽ�У�D1D2����ֱ����ֱ��BC��ľ���Ϊ2![]() ����D1D2��ֱ�߽���ʽΪy����x+b����b��3��4������y����x+7���������������������鼴����D1��D2�����ꣻT1��T2��T3��T4��T5��ֱ��BC�ľ���Ϊ
����D1D2��ֱ�߽���ʽΪy����x+b����b��3��4������y����x+7���������������������鼴����D1��D2�����ꣻT1��T2��T3��T4��T5��ֱ��BC�ľ���Ϊ![]() ������BCƽ�е�ֱ��Ϊy����x+t����|t��3|��
������BCƽ�е�ֱ��Ϊy����x+t����|t��3|��![]() ���������ֱ���ֱ��y����x+
���������ֱ���ֱ��y����x+![]() ��y����x+
��y����x+![]() �ϣ��ٽ�ֱ����M��N�Ľ���ʽ�������������꣮
�ϣ��ٽ�ֱ����M��N�Ľ���ʽ�������������꣮
�⣺��1����N��Mͼ���·��IJ��ֹ���x��Գƣ�
��N���ں�������ʽΪy����x2+2x+3��
��2����x2��2x��3��0�����x����1��x��3��
��A����1��0����B��3��0����
������N��y���ڵ�C��
��C��0��3����
�ֱ���BC��AB�Ĵ�ֱƽ���߽��ڵ�O'����O'Ϊ��ABC�����Բ��
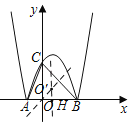
��Rt��BOCΪ����ֱ�������Σ�
��OO'��OH��O'H��1��
��HB��2��
��O'B��![]() ��
��
��O'B�ǡ�ABC���Բ�İ뾶��
���ABC���Բ�������5����
��3����P����M��ʱ����P��m��m2��2m��3����Q��n��0����
��m��3��m�ܩ�1��
����BQ��PC��BQ��PCʱ��B��C���е�Ϊ��![]() ��
��![]() ����P��Q���е�Ϊ��
����P��Q���е�Ϊ��![]() ��
��![]() ����
����
��![]() ��
��![]() �����m��1+
�����m��1+![]() ��m��1��
��m��1��![]() ��
��
![]() ��
��![]() �����n��2��
�����n��2��![]() ��n��2+
��n��2+![]() ��
��
��Q��2��![]() ��0����Q��2+
��0����Q��2+![]() ��0����
��0����
����BP��CQ��BP��CQʱ��B��Q���е�Ϊ��![]() ��0����P��C���е�Ϊ��
��0����P��C���е�Ϊ��![]() ��
��![]() ����
����
��![]() ��0�����m��0��m��2���������ϣ���
��0�����m��0��m��2���������ϣ���
��P����N��ʱ����P��m����m2+2m+3����Q��n��0����
�ੁ1��m��3��
����BQ��PC��BQ��PCʱ��B��C���е�Ϊ��![]() ��
��![]() ����P��Q���е�Ϊ��
����P��Q���е�Ϊ��![]() ��
��![]() ����
����
��![]() ��
��![]() �����m��0��m��2��
�����m��0��m��2��
![]() ��
��![]() �����n��3��n��1��
�����n��3��n��1��
��Q��1��0����Q��3��0����
��Q��3��0����B��3��0���غϣ�
��Q��1��0����
����BP��CQ��BP��CQʱ��B��Q���е�Ϊ��![]() ��0����P��C���е�Ϊ��
��0����P��C���е�Ϊ��![]() ��
��![]() ����
����
��![]() ��0�����m��1+
��0�����m��1+![]() ��m��1��
��m��1��![]() ���������ϣ���
���������ϣ���
����������Q��1��0����Q��2��![]() ��0����Q��2+
��0����Q��2+![]() ��0��ʱ�Ե�B��C��P��QΪ������ı�����ƽ���ı��Σ�
��0��ʱ�Ե�B��C��P��QΪ������ı�����ƽ���ı��Σ�
��4����![]() ��
��![]() ��S��ABC��
��S��ABC��
��D1D2����ֱ����ֱ��BCƽ�У�
��BC��3![]() ��
��
��A�㵽BC�ľ���Ϊh��
�ߡ�ABC�������![]() ��3
��3![]() h��
h��![]() ��4��3��
��4��3��
��h��2![]() ��
��
��D1D2����ֱ����ֱ��BC��ľ���Ϊ2![]() ��
��
��D1D2��ֱ�߽���ʽΪy����x+b��
��b��3��4��
��b��7��
��y����x+7��
����![]() �����x��
�����x��![]() ��x��
��x��![]() ��
��
��D1��![]() ��
��![]() ����D2��
����D2��![]() ��
��![]() ����
����
����![]() �����x�⣻
�����x�⣻
����������D1��![]() ��
��![]() ����D2��
����D2��![]() ��
��![]() ����
����
��T1��T2��T3��T4��T5���B��CΧ�ɵ������ε����Ϊ![]() ��
��
��T1��T2��T3��T4��T5��ֱ��BC�ľ���Ϊ![]() ��
��
����BCƽ�е�ֱ��Ϊy����x+t��
��|t��3|��![]() ��
��
��t��![]() ��t��
��t��![]() ��
��
��y����x+![]() ��y����x+
��y����x+![]() ��
��
������M��ʱ��x��3��x�ܩ�1��
����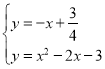 �����x��
�����x��![]() ��x����
��x����![]() ��
��
��x����![]() ��
��
��T1����![]() ��
��![]() ����
����
����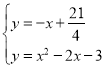 �����x��
�����x��![]() ��x��
��x��![]() ��
��
��T2��![]() ��
��![]() ����T3��
����T3��![]() ��
��![]() ����
����
������N��ʱ����1��x��3��
����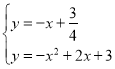 �����x��
�����x��![]() ���ᣩ��x��
���ᣩ��x��![]() ��
��
��T4��![]() ��
��![]() ����
����
����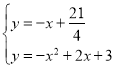 �����x��
�����x��![]() ��
��
��T5��![]() ��
��![]() ����
����
�����������������������������ֱ���T1����![]() ��
��![]() ����T2��
����T2��![]() ��
��![]() ����T3��
����T3��![]() ��
��![]() ����T4��
����T4��![]() ��
��![]() ����T5��
����T5��![]() ��
��![]() ����
����


 ��Կ���Ծ�ϵ�д�
��Կ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD��PΪ����AB�ϵ�һ�㣬��BPΪ����������BPEF��ʹ��F���߶�CB���ӳ����ϣ�����EA��EC��
��1����ͼ1������P���߶�AB���ӳ����ϣ���֤��EA=EC��
��2������P���߶�AB�ϣ���ͼ2������PΪAB���е�ʱ���ж���ACE����״����˵�����ɣ�
��3���ڣ�1���������£���������ABCD�̶���������BPEF�Ƶ�B��תһ�ܣ���AB=4��BP=a��������ת��������ACE�������СֵΪ4����ֱ��д��a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
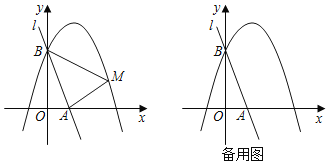
����Ŀ����ͼ��ֱ��l��y����3x+3��x�ᡢy��ֱ��ཻ��A��B���㣬������y��ax2��2ax+a+4��a��0��������B��
��1����������ߵĺ�������ʽ��
��2����֪��M���������ϵ�һ�����㣬���ҵ�M�ڵ�һ�����ڣ�����AM��BM�����M�ĺ�����Ϊm����ABM�����ΪS����S��m�ĺ�������ʽ�������S�����ֵ��
��3���ڣ�2���������£���Sȡ�����ֵʱ������M��Ӧ��λ�ü�Ϊ��M�䣮д����M������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱ���ABC�ı߳���2��D��E�ֱ�ΪAB��AC���е㣬�ӳ�BC����F��ʹCF=![]() BC������CD��EF��
BC������CD��EF��
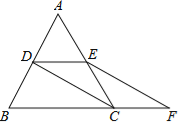
��1����֤��DE=CF��
��2����EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
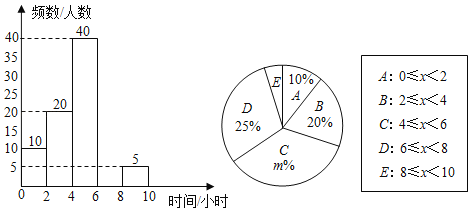
����Ŀ��ij��ѧΪ�˽�ѧ��ÿ�ܵĿ����Ķ�ʱ��������������˲���ѧ������ѧ��ÿ�ܵĿ����Ķ�ʱ��x����λ��Сʱ�����з������������Ƴ���ͼ��ʾ�IJ�������Ƶ���ֲ�ֱ��ͼ������ͳ��ͼ��
��1��������ͳ��ͼ�У�m���� ����E������Ӧ�����ε�Բ�ĽǶ���Ϊ�� ����
��2��E����3��Ůͬѧ��2����ͬѧ��ѧУ����E���2��ͬѧȥ�μ�ȫ�о��еľ����ж���������鵽1��Ůͬѧ��1����ͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽�ijУѧ���������ĸ����ӽ�Ŀ��![]() ��ǿ����
��ǿ����![]() ��
��![]() �й�ʫ�ʴ��
�й�ʫ�ʴ��![]() ��
��![]() �ʶ���
�ʶ���![]() ��
��![]() �������
�����й���![]() ��ϲ������������ȡ�˲���ѧ�����е��飬Ҫ��ÿ��ѧ��ѡ������ֻ��ѡ��һ���Լ���ϲ���Ľ�Ŀ�����ݵ�����������������������������ͳ��ͼ��
��ϲ������������ȡ�˲���ѧ�����е��飬Ҫ��ÿ��ѧ��ѡ������ֻ��ѡ��һ���Լ���ϲ���Ľ�Ŀ�����ݵ�����������������������������ͳ��ͼ��

�������ͼ�����ṩ����Ϣ������������⣺
![]() ���ε����ѧ������Ϊ______��
���ε����ѧ������Ϊ______��
![]() ������ͳ��ͼ�У�A������ռԲ�ĽǵĶ���Ϊ______��
������ͳ��ͼ�У�A������ռԲ�ĽǵĶ���Ϊ______��
![]() �뽫����ͳ��ͼ����������
�뽫����ͳ��ͼ����������
![]() ����У����3000��ѧ�������Ƹ�У��ϲ��
����У����3000��ѧ�������Ƹ�У��ϲ��![]() �й�ʫ�ʴ��
�й�ʫ�ʴ��![]() ��ѧ���ж�������
��ѧ���ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ���Ź��ŵĽ���ͼ�������Ŷ�����������������״����ˮ��Ŀ���Ϊ10mʱ���Ŷ���ˮ��
����������5m��
��1������������ͬѧ�ǵó����ֽ���ƽ��ֱ������ϵ�ķ���������ͼ��
��ѡ��ķ�����_____�����һ��������������������B��������______���������ѡ�����е������ߵı���ʽ��
��2����Ϊ����ˮ��й����ˮ����ȱ�Ϊ6m����ˮ�����ǵĸ߶���


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���E��BC���ϣ�AE=AB�����߶�AC�Ƶ�A��ת��AF��λ�ã�ʹ�á�CAF=��BAE.����EF��EF��AC���ڵ�G��

(1)��֤��EF =BC��
(2)����ABC=65�㣬��ACB=28�㣬���FGC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�
��ͼ1.�ڡ�ABC�У���A����B����C���Եı߷ֱ�Ϊa��b��c�����Եõ���
![]()
֤��������A��AD��BC������ΪD��
��Rt��ABD��![]()
��![]()
��![]()
ͬ����![]()
![]()
��![]()
��1��ͨ����������֤����
![]()
��2�����ã�1���еĽ��۽�����⣺
��ͼ2����![]() �У�
�У�![]() ����AC�ij��ȣ�
����AC�ij��ȣ�
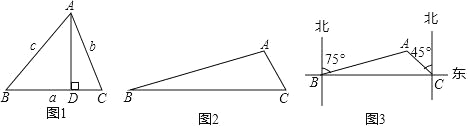
��3����ͼ3��Ϊ�˿�����·�Եij��лĵأ�������Աѡ��A��B��C���������㣬��B����A�ڱ�ƫ��75�㷽���ϣ��ر�ֱ��·������������ʻ18km����C�㣬���A�ڱ�ƫ��45�㷽���ϣ�����������Ϣ����A��B��C����Χ�ɵ������ε������
������ο���ֵ��sin15���0.3��sin120���0.9��![]() ��1.4�����ȡ������
��1.4�����ȡ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com