
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:初中数学 来源: 题型:解答题
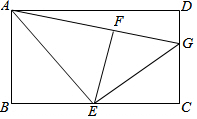 如图,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.
如图,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
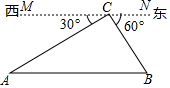 由干早年铁路建设技术不发达,只能从A地先到C地,再到B地,由于现在技术的提升,可以建设一条直接从A地到B地的公路,A,B,C三地位置关系如图所示,MN∥AB,AC=6km,BC=2$\sqrt{3}$km,
由干早年铁路建设技术不发达,只能从A地先到C地,再到B地,由于现在技术的提升,可以建设一条直接从A地到B地的公路,A,B,C三地位置关系如图所示,MN∥AB,AC=6km,BC=2$\sqrt{3}$km,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图抛物线y=ax2+bx+c与x轴交于A、B两点,其中B点坐标为(4,0),直线DE是抛物线的对称轴,且与x轴交于点E,CD⊥DE于D,现有下列结论:
如图抛物线y=ax2+bx+c与x轴交于A、B两点,其中B点坐标为(4,0),直线DE是抛物线的对称轴,且与x轴交于点E,CD⊥DE于D,现有下列结论:| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①② |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com