
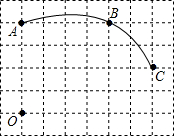
 ��ͼ���ڵ�λ����Ϊ1�������������У�һ��Բ���������A��B��C��
��ͼ���ڵ�λ����Ϊ1�������������У�һ��Բ���������A��B��C������ ��1���������⽨��ƽ��ֱ������ϵ��Ȼ��������AB�Ĵ�ֱƽ���ߣ��Լ�BC�Ĵ�ֱƽ���ߣ���ֱ�ߵĽ��㼴ΪԲ��D������AD��CD��
��2���ٸ��ݵ�һ�ʻ�����ͼ�μ��ɵó�C��D�����ꣻ
����ֱ��������AOD�У���OA��OD�ij������ù��ɶ������AD�ij�����ΪԲO�İ뾶��
��ֱ��CE��ԲO��λ�ù�ϵ�����У�����Ϊ����Բ�İ뾶�ó�DC�ij�����ֱ��������CEF�У���CF��FE�ij������ù��ɶ������CE�ij�������DE�ij������ù��ɶ������涨���ó�������DCEΪֱ�������Σ���EC��ֱ��DC���ɵó�ֱ��CEΪԲO�����ߣ�
��� �⣺��1���������⻭����Ӧ��ͼ�Σ���ͼ��ʾ��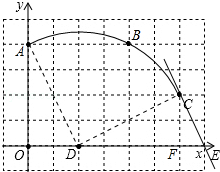
��2������Rt��AOD��OA=4��OD=2��
���ݹ��ɶ����ã�AD=$\sqrt{O{A}^{2}+O{D}^{2}}$=2$\sqrt{5}$��
���D�İ뾶Ϊ2$\sqrt{5}$��
��AC=$\sqrt{{2}^{2}+{6}^{2}}$=2$\sqrt{10}$��CD=2$\sqrt{5}$��
AD2+CD2=AC2��
���ADC=90�㣮
����ADC�Ļ���=$\frac{90�С�2\sqrt{5}}{180}$=$\sqrt{5}$�У�
Բ�ĵ���İ뾶=$\frac{\sqrt{5}}{2}$��
��ֱ��EC���D��λ�ù�ϵΪ���У�
����Ϊ����Rt��CEF�У�CF=2��EF=1��
���ݹ��ɶ����ã�CE=$\sqrt{C{F}^{2}+E{F}^{2}}$=$\sqrt{5}$��
�ڡ�CDE�У�CD=2$\sqrt{5}$��CE=$\sqrt{5}$��DE=5��
��CE2+CD2=��$\sqrt{5}$��2+��2$\sqrt{5}$��2=5+20=25��DE2=25��
��CE2+CD2=DE2��
���CDEΪֱ�������Σ�����DCE=90�㣬
��CE��ԲD���У�
���� ���⿼����ֱ����Բ��λ�ù�ϵ���漰��֪ʶ�У�������ͼ�����ʣ��������������ɶ������涨�������ߵ��ж������������ν�ϵ�˼�룬�������⻭����Ӧ��ͼ���ǽⱾ��Ĺؼ���


 �ִʾ��ƪϵ�д�
�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��������� | B�� | ֱ�������� | C�� | �۽������� | D�� | ���������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢� | B�� | �� | C�� | �ڢ� | D�� | �ۢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AB�ǰ�ԲO��ֱ����C��D�ǰ�ԲO�ϵ����㣬��OD��BC��OD��AC���ڵ�E��
��ͼ��AB�ǰ�ԲO��ֱ����C��D�ǰ�ԲO�ϵ����㣬��OD��BC��OD��AC���ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6�� | B�� | 5�� | C�� | 4�� | D�� | 3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com