
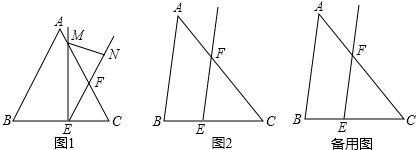
分析 (1)根据平行线得出∠FEC=∠B=80°,根据三角形内角和定理求出∠A、∠C,求出∠EMN和∠EMC,即可求出答案;
(2)分为两种情况:①当点M在AF上时,根据平行线得出∠FEC=∠B=α,根据三角形内角和定理求出∠C,根据三角形内角和定理求出∠EMN和∠EMC,即可求出答案;②当点M在CF上时,由①得出∠C=$\frac{1}{2}$(180°-α),∠EMN=90°-$\frac{1}{2}$β,代入∠FMN+∠EMN=∠MEC+∠C得出∠FMN+90°-$\frac{1}{2}$β=α-β+$\frac{1}{2}$(180°-α),即可求出答案.
解答 解:(1)∵EF∥AB,
∴∠B=∠FEC=80°,∠A=∠EFC,
∵∠A=∠C,
∴∠C=∠A=$\frac{1}{2}$(180°-∠FEC)=50°,
∵EF∥AB,
∴∠EFC=∠A=50°.
∵∠MEF=β=30°,
∴∠EMN=∠ENM=$\frac{1}{2}$(180°-30°)=75°,∠EMF=∠EFC-∠MEF=50°-30°=20°.
∴∠FMN=∠EMN-∠EMF=75°-20°=55°;
(2)①当点M在AF上时,∠FMN=$\frac{1}{2}$α+$\frac{1}{2}$β,
如图1,∵EF∥AB,
∴∠FEC=∠B=α,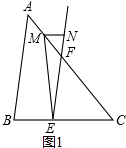
∵∠A=∠C,
∴∠C=$\frac{1}{2}$(180°-α),
∵∠EMN=∠ENM,
∴∠EMN=$\frac{1}{2}$(180°-β)=90°-$\frac{1}{2}$β,
∠MEC=∠FEC+∠MEN=α+β,
∴∠EMC=180°-∠MEC-∠C
=180°-(α+β)-$\frac{1}{2}$(180°-α)
=90°-$\frac{1}{2}$α-β,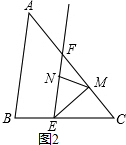
∴∠FMN=∠EMN-∠EMC
=(90°-$\frac{1}{2}$β)-(90°-$\frac{1}{2}$α-β)=$\frac{1}{2}$α+$\frac{1}{2}$β;
②当点M在CF上时,∠FMN=$\frac{1}{2}$α-$\frac{1}{2}$β,
理由是:如图3,由①得:∠C=$\frac{1}{2}$(180°-α),∠EMN=90°-$\frac{1}{2}$β,
∠FMN+∠EMN=∠MEC+∠C,
即∠FMN+90°-$\frac{1}{2}$β=α-β+$\frac{1}{2}$(180°-α),
∴∠FMN=$\frac{1}{2}$α-$\frac{1}{2}$β.
点评 本题考查了平行线的性质、三角形内角和定理和三角形外角性质的应用,主要考查学生运用定理进行推理和计算的能力.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案科目:初中数学 来源: 题型:解答题
 如图,⊙O的直径AB=10,CD是⊙O的弦,AC与BD相交于点P.
如图,⊙O的直径AB=10,CD是⊙O的弦,AC与BD相交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
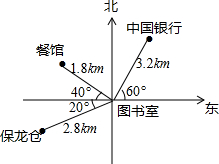 如图,表示的是图书馆、保龙仓、中国银行和餐馆的位置关系.
如图,表示的是图书馆、保龙仓、中国银行和餐馆的位置关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com