
【题目】已知,如图,在![]() ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
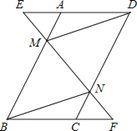
(1)求证:△AEM≌△CFN;
(2)求证:四边形BMDN是平行四边形.
【答案】证明见解析
【解析】
(1)根据平行四边形的性质可得出AD∥BC,∠DAB=∠BCD,再根据平行线的性质及补角的性质得出∠E=∠F,∠EAM=∠FCN,从而利用ASA可作出证明.
(2)根据平行四边形的性质及(1)的结论可得BM![]() DN,则由有一组对边平行且相等的四边形是平行四边形即可证明.
DN,则由有一组对边平行且相等的四边形是平行四边形即可证明.
证明:(1) ∵四边形ABCD是平行四边形,∴AB∥DC ,AD∥BC.
∴∠E=∠F,∠DAB=∠BCD.
∴∠EAM=∠FCN.
又∵AE=CF
∴△AEM≌△CFN(ASA).
(2) ∵由(1)△AEM≌△CFN
∴AM=CN.
又∵四边形ABCD是平行四边形
∴AB![]() CD
CD
∴BM![]() DN.
DN.
∴四边形BMDN是平行四边形.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BC=4,面积是16,AC的垂直平分线EF分别交AC,AB边于点E、F,若点D为BC边上的中点,点M为线段EF一动点,则△CDM周长的最小值为( )
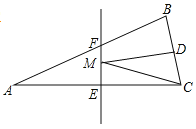
A.4B.8C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题解决)
一节数学课上,老师提出了这样一个问题:如图1,点P是正方形ABCD内一点,PA=1,PB=2,PC=3.你能求出∠APB的度数吗?
小明通过观察、分析、思考,形成了如下思路:
思路一:将△BPC绕点B逆时针旋转90°,得到△BP′A,连接PP′,求出∠APB的度数;
思路二:将△APB绕点B顺时针旋转90°,得到△CP'B,连接PP′,求出∠APB的度数.
请参考小明的思路,任选一种写出完整的解答过程.
(类比探究)
如图2,若点P是正方形ABCD外一点,PA=3,PB=1,PC=![]() ,求∠APB的度数.
,求∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
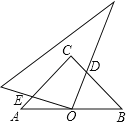
【题目】如图,在Rt△ABC中,∠C=90°.点O是AB的中点,边AC=6,将边长足够大的三角板的直角顶点放在点O处,将三角板绕点0旋转,始终保持三角板的直角边与AC相交,交点为点E,另条直角边与BC相交,交点为D,则等腰直角三角板的直角边被三角板覆盖部分的两条线段CD与CE的长度之和为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长均为1的方格纸中有线段AB,其中点A、B均在小正方形的顶点上.
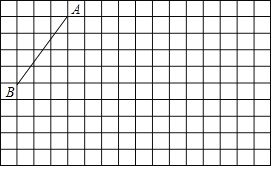
(1)在方格纸中画出以BC为底的钝角等腰三角形ABC,且点C在小正方形的顶点上;
(2)将(1)中的△ABC绕点C逆时针旋转90°得到△DEC(点A的对应点是点D,点B的对应点是点E),画出△CDE;
(3)在(2)的条件下,连接BE,请直接写出△BCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一条抛物线![]() 与
与![]() 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
(1)“抛物线三角形”一定是 三角形;
(2)若抛物线![]() 的“抛物线三角形”是等腰直角三角形,求
的“抛物线三角形”是等腰直角三角形,求![]() 的值;
的值;
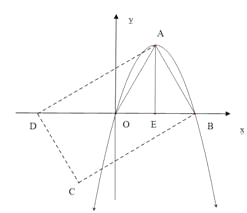
(3)如图,△![]() 是抛物线
是抛物线![]() 的“抛物线三角形”,是否存在以原点
的“抛物线三角形”,是否存在以原点![]() 为对称中心的矩形
为对称中心的矩形![]() ?若存在,求出过
?若存在,求出过![]() 三点的抛物线的表达式;若不存在,说明理由.
三点的抛物线的表达式;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D.再分别以点C、D为圆心,大于![]() CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是
CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是

A.射线OE是∠AOB的平分线
B.△COD是等腰三角形
C.C、D两点关于OE所在直线对称
D.O、E两点关于CD所在直线对称
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=6,BC=8.
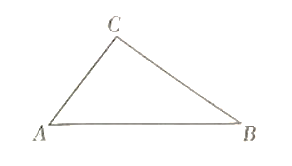
(1)用直尺和圆规作∠A的平分线,交BC于点D;(要求:不写作法,保留作图痕迹)
(2)求S△ADC: S△ADB的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com