
【题目】如图,在△ABC中,AB=AC,BC=4,面积是16,AC的垂直平分线EF分别交AC,AB边于点E、F,若点D为BC边上的中点,点M为线段EF一动点,则△CDM周长的最小值为( )
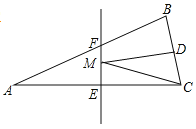
A.4B.8C.10D.12
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图.一次函数y=![]() x+1的图象L1交y轴于点A,一次函数y=﹣x+3的图象L2交x轴于点B,L1与L2交于点C.
x+1的图象L1交y轴于点A,一次函数y=﹣x+3的图象L2交x轴于点B,L1与L2交于点C.
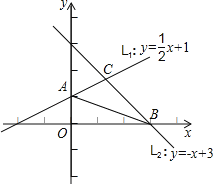
(1)求点A与点B的坐标;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知一次函数![]() 的图像与x轴交于点
的图像与x轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.

(1)求直线![]() 的解析式;
的解析式;
(2)在坐标系中能否找到点![]() ,使得
,使得![]() 且
且![]() ?如果能,求出满足条件的点
?如果能,求出满足条件的点![]() 的坐标;如果不能,请说明理由.
的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,AC是⊙O的直径,OB是⊙O的半径,PA切⊙O于点A,PB与AC的延长线交于点M,∠COB=∠APB.
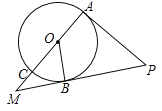
(1)求证:PB是⊙O的切线;
(2)当OB=3,PA=6时,求MB,MC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,∠ABC=45°,AD是⊙O的切线交BC的延长线于D,AB交OC于E.
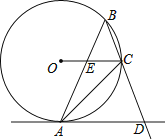
(1)求证:AD∥OC;
(2)若AE=2![]() ,CE=2.求⊙O的半径和线段BE的长.
,CE=2.求⊙O的半径和线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
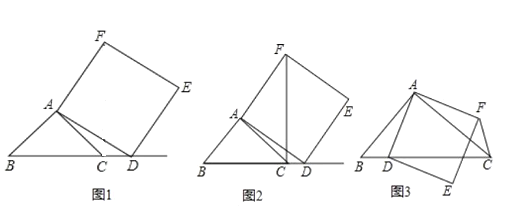
【题目】如图①,在△ABC中,![]() 为锐角,点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
为锐角,点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如图②,如果AB=AC,![]() ,当点D在线段BC的延长线上时,猜想线段CF、BD的关系,并说明理由.
,当点D在线段BC的延长线上时,猜想线段CF、BD的关系,并说明理由.
(2)如图③,如果AB![]() AC,
AC,![]() 是锐角,点D在线段BC上,当
是锐角,点D在线段BC上,当![]() 时,必有CF
时,必有CF![]() BC(点C,F不重合),请先在横线上添加条件,再作证明.
BC(点C,F不重合),请先在横线上添加条件,再作证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
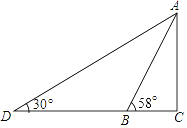
【题目】如图,某游乐园有一个滑梯高度AB,高度AC为3米,倾斜角度为58°.为了改善滑梯AB的安全性能,把倾斜角由58°减至30°,调整后的滑梯AD比原滑梯AB增加多少米?(精确到0.1米)
(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两队参加了“端午情,龙舟韵”赛龙舟比赛,两队在比赛时的路程![]() (米)与时间
(米)与时间![]() (秒)之间的函数图象如图所示,请你根据图象判断,下列说法正确的是( )
(秒)之间的函数图象如图所示,请你根据图象判断,下列说法正确的是( )
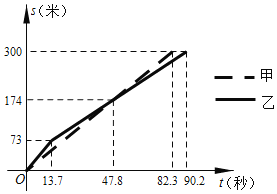
A. 乙队率先到达终点
B. 甲队比乙队多走了![]() 米
米
C. 在![]() 秒时,两队所走路程相等
秒时,两队所走路程相等
D. 从出发到![]() 秒的时间段内,乙队的速度慢
秒的时间段内,乙队的速度慢
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在![]() ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
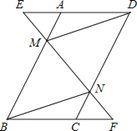
(1)求证:△AEM≌△CFN;
(2)求证:四边形BMDN是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com