
【题目】如图,⊙O是△ABC的外接圆,∠ABC=45°,AD是⊙O的切线交BC的延长线于D,AB交OC于E.
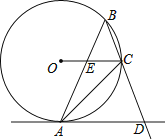
(1)求证:AD∥OC;
(2)若AE=2![]() ,CE=2.求⊙O的半径和线段BE的长.
,CE=2.求⊙O的半径和线段BE的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连结OA,根据切线的性质得到OA⊥AD,再根据圆周角定理得到∠AOC=2∠ABC=90°,然后根据平行线的判定即可得到结论;
(2)设⊙O的半径为R,则OA=R,OE=R-2,AE=2![]() ,在Rt△OAE中根据勾股定理可计算出R=4;作OH⊥AB于H,根据垂径定理得AH=BH,再利用面积法计算出OH=
,在Rt△OAE中根据勾股定理可计算出R=4;作OH⊥AB于H,根据垂径定理得AH=BH,再利用面积法计算出OH=![]() ,然后根据勾股定理计算出AH=
,然后根据勾股定理计算出AH=![]() ,则HE=AE-AH=2
,则HE=AE-AH=2![]() -
-![]() =
=![]() ,再利用BE=BH-HE进行计算.
,再利用BE=BH-HE进行计算.
试题解析:(1)连结OA,如图,
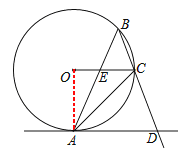
∵AD是⊙O的切线,
∴OA⊥AD,
∵∠AOC=2∠ABC=2×45°=90°,
∴OA⊥OC,
∴AD∥OC;
(2)设⊙O的半径为R,则OA=R,OE=R-2,AE=2![]() ,
,
在Rt△OAE中,∵AO2+OE2=AE2,
∴R2+(R-2)2=(2![]() )2,解得R=4,
)2,解得R=4,
作OH⊥AB于H,如图,OE=OC-CE=4-2=2,
则AH=BH,
∵![]() OHAE=
OHAE=![]() OEOA,
OEOA,
∴OH=![]() =
=![]() ,
,
在Rt△AOH中,AH=![]() ,
,
∴HE=AE-AH=2![]() -
-![]() =
=![]()
∴BH=![]() ,
,
∴BE=BH-HE=![]() -
-![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】“六一”儿童节前夕,某县教育局准备给留守儿童赠送一批学习用品,先对红星小学的留守儿童人数进行抽样统计,发现各班留守儿童人数分别为6名,7名,8名,10名,12名这五种情形,并绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
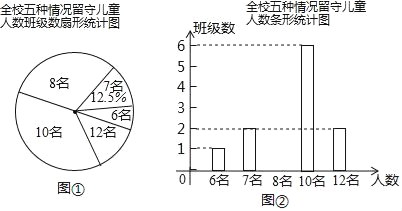
(1)该校有_____个班级,补全条形统计图;
(2)求该校各班留守儿童人数数据的平均数,众数与中位数;
(3)若该镇所有小学共有60个教学班,请根据样本数据,估计该镇小学生中,共有多少名留守儿童.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数y=ax2+bx+c的图象,在下列说法中:①ac<0;②a+b+c>0;③方程ax2+bx+c=0的根是x1=﹣1,x2=3; ④b2﹣4ac>0;⑤当x>1时,y随x的增大而增大;正确的说法有( )
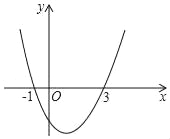
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,DE平分∠ADB,则∠B=( )
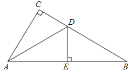
A. 40° B. 30° C. 25° D. 22.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若OC=3,OA=5,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BC=4,面积是16,AC的垂直平分线EF分别交AC,AB边于点E、F,若点D为BC边上的中点,点M为线段EF一动点,则△CDM周长的最小值为( )
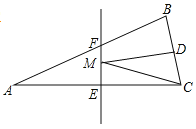
A.4B.8C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
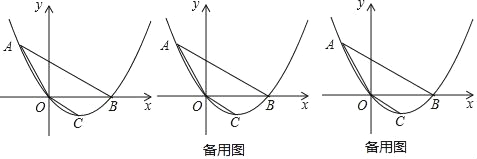
【题目】如图,顶点为C的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,连接OC、OA、AB,已知OA=OB=2,∠AOB=120°.
(1)求这条抛物线的表达式;
(2)过点C作CE⊥OB,垂足为E,点P为y轴上的动点,若以O、C、P为顶点的三角形与△AOE相似,求点P的坐标;
(3)若将(2)的线段OE绕点O逆时针旋转得到OE′,旋转角为α(0°<α<120°),连接E′A、E′B,求E′A+![]() E′B的最小值.
E′B的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形![]() 的边长为4,点
的边长为4,点![]() 是△
是△![]() 的中心,
的中心,![]() .绕点
.绕点![]() 旋转
旋转![]() ,分别交线段
,分别交线段![]() 于
于![]() 两点,连接
两点,连接![]() ,给出下列四个结论:①
,给出下列四个结论:①![]() ;②
;②![]() ;③四边形
;③四边形![]() 的面积始终等于
的面积始终等于![]() ;④△
;④△![]() 周长的最小值为6,上述结论中正确的个数是( )
周长的最小值为6,上述结论中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长均为1的方格纸中有线段AB,其中点A、B均在小正方形的顶点上.
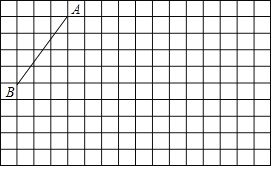
(1)在方格纸中画出以BC为底的钝角等腰三角形ABC,且点C在小正方形的顶点上;
(2)将(1)中的△ABC绕点C逆时针旋转90°得到△DEC(点A的对应点是点D,点B的对应点是点E),画出△CDE;
(3)在(2)的条件下,连接BE,请直接写出△BCE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com