
ЁОЬтФПЁПЁАСљвЛЁБЖљЭЏНкЧАЯІЃЌФГЯиНЬг§ОжзМБИИјСєЪиЖљЭЏдљЫЭвЛХњбЇЯАгУЦЗЃЌЯШЖдКьаЧаЁбЇЕФСєЪиЖљЭЏШЫЪ§НјааГщбљЭГМЦЃЌЗЂЯжИїАрСєЪиЖљЭЏШЫЪ§ЗжБ№ЮЊ6УћЃЌ7УћЃЌ8УћЃЌ10УћЃЌ12УћетЮхжжЧщаЮЃЌВЂЛцжЦГіШчЯТЕФЭГМЦЭМЂйКЭЭМЂкЃЎЧыИљОнЯрЙиаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
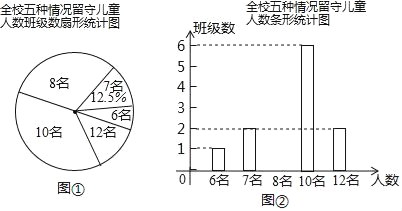
ЃЈ1ЃЉИУаЃга_____ИіАрМЖЃЌВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉЧѓИУаЃИїАрСєЪиЖљЭЏШЫЪ§Ъ§ОнЕФЦНОљЪ§ЃЌжкЪ§гыжаЮЛЪ§ЃЛ
ЃЈ3ЃЉШєИУеђЫљгааЁбЇЙВга60ИіНЬбЇАрЃЌЧыИљОнбљБОЪ§ОнЃЌЙРМЦИУеђаЁбЇЩњжаЃЌЙВгаЖрЩйУћСєЪиЖљЭЏЃЎ
ЁОД№АИЁПЃЈ1ЃЉ16ЃЛЃЈ2ЃЉЦНОљЪ§ЪЧ9ЃЌжкЪ§ЪЧ10ЃЌжаЮЛЪ§ЪЧ9ЃЛЃЈ3ЃЉ540ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнга7УћСєЪиЖљЭЏАрМЖга2ИіЃЌЫљеМЕФАйЗжБШЪЧ12.5%ЃЌМДПЩЧѓЕУАрМЖЕФзмИіЪ§ЃЌдйЧѓГіга8УћСєЪиЖљЭЏАрМЖЕФИіЪ§ЃЌНјЖјВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉНЋетзщЪ§ОнАДееДгаЁЕНДѓХХСаМДПЩЧѓЕУЭГМЦЕФетзщСєЪиЖљЭЏШЫЪ§Ъ§ОнЕФЦНОљЪ§ЁЂжкЪ§КЭжаЮЛЪ§ЃЛ
ЃЈ3ЃЉРћгУАрМЖЪ§60ГЫвдЃЈ2ЃЉжаЧѓЕУЕФЦНОљЪ§МДПЩЃЎ
ЃЈ1ЃЉИУаЃЕФАрМЖЪ§ЪЧЃК2ЁТ12.5%=16ЃЈИіЃЉЃЎ
дђШЫЪ§ЪЧ8УћЕФАрМЖЪ§ЪЧЃК16Љ1Љ2Љ6Љ2=5ЃЈИіЃЉЃЎ
ЬѕаЮЭГМЦЭМВЙГфШчЯТЭМЫљЪОЃК
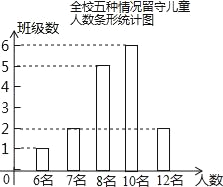
ЙЪД№АИЮЊЃК16ЃЛ
ЃЈ2ЃЉУПАрЕФСєЪиЖљЭЏЕФЦНОљЪ§ЪЧЃКЃЈ1ЁС6+2ЁС7+5ЁС8+6ЁС10+12ЁС2ЃЉЁТ16=9
НЋетзщЪ§ОнАДееДгаЁЕНДѓХХСаЪЧЃК6ЃЌ7ЃЌ7ЃЌ8ЃЌ8ЃЌ8ЃЌ8ЃЌ8ЃЌ10ЃЌ10ЃЌ10ЃЌ10ЃЌ10ЃЌ10ЃЌ12ЃЌ12ЃЎ
ЙЪетзщЪ§ОнЕФжкЪ§ЪЧ10ЃЌжаЮЛЪ§ЪЧЃЈ8+10ЃЉЁТ2=9ЃЎ
МДЭГМЦЕФетзщСєЪиЖљЭЏШЫЪ§Ъ§ОнЕФЦНОљЪ§ЪЧ9ЃЌжкЪ§ЪЧ10ЃЌжаЮЛЪ§ЪЧ9ЃЛ
ЃЈ3ЃЉИУеђаЁбЇЩњжаЃЌЙВгаСєЪиЖљЭЏ60ЁС9=540ЃЈУћЃЉЃЎ
Д№ЃКИУеђаЁбЇЩњжаЙВгаСєЪиЖљЭЏ540УћЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
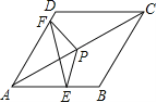
ЁОЬтФПЁПШчЭМЃЌАбЁїEFPАДЭМЪОЗНЪНЗХжУдкСтаЮABCDжаЃЌЪЙЕУЖЅЕуEЁЂFЁЂPЗжБ№дкЯпЖЮABЁЂADЁЂACЩЯЃЌвбжЊEPЃНFPЃН4ЃЌEFЃН4![]() ЃЌЁЯBADЃН60ЁуЃЌЧвABЃО4
ЃЌЁЯBADЃН60ЁуЃЌЧвABЃО4![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЁЯEPFЕФДѓаЁЃЛ
ЃЈ2ЃЉШєAP=6ЃЌЧѓAEЃЋAFЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌАбRtЁїABCЗХдкжБНЧзјБъЯЕФкЃЌЦфжаЁЯCABЃН90ЁуЃЌBCЃН5ЃЌЕуAЃЌBЕФзјБъЗжБ№ЮЊ(1ЃЌ0)ЃЌ(4ЃЌ0)ЃЌНЋЁїABCбиxжсЯђгвЦНвЦЃЌЕБЕуCТфдкжБЯпyЃН2xЃ6ЩЯЪБЃЌЯпЖЮBCЩЈЙ§ЕФУцЛ§ЮЊ________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ![]() ЃЌХзЮяЯп
ЃЌХзЮяЯп![]() гыжБЯп
гыжБЯп![]() НЛгк
НЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌЙ§
СНЕуЃЌЙ§![]() зї
зї![]() жсНЛХзЮяЯпгкЕу
жсНЛХзЮяЯпгкЕу![]() ЃЌжБЯп
ЃЌжБЯп![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() ЃЎ
ЃЎ
![]() Чѓ
Чѓ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() Ш§ЕуЕФзјБъЃЛ
Ш§ЕуЕФзјБъЃЛ
![]() ШєЕу
ШєЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЩЯЕФвЛИіЖЏЕуЃЌЙ§
ЩЯЕФвЛИіЖЏЕуЃЌЙ§![]() зї
зї![]() жсНЛХзЮяЯпгк
жсНЛХзЮяЯпгк![]() ЕуЃЌСЌНг
ЕуЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
![]() ШчЭМ
ШчЭМ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() МА
МА![]() ЃЌЩшЕу
ЃЌЩшЕу![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌЕу
ЕФжаЕуЃЌЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЩЯШЮвтвЛЕуЃЌНЋ
ЩЯШЮвтвЛЕуЃЌНЋ![]() биБп
биБп![]() ЗелЕУЕН
ЗелЕУЕН![]() ЃЌЧѓЕБ
ЃЌЧѓЕБ![]() ЮЊКЮжЕЪБЃЌ
ЮЊКЮжЕЪБЃЌ![]() гы
гы![]() жиЕўВПЗжЕФУцЛ§ЪЧ
жиЕўВПЗжЕФУцЛ§ЪЧ![]() УцЛ§ЕФ
УцЛ§ЕФ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкБпГЄЮЊ3ЕФе§ЗНаЮABCDжаЃЌЕуEЪЧBCБпЩЯЕФЕуЃЌEC=2ЃЌЁЯAEP=90ЁуЃЌЧвEPНЛе§ЗНаЮЭтНЧЕФЦНЗжЯпCPгкЕуPЃЌдђPCЕФГЄЮЊ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
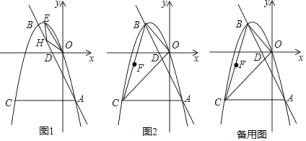
ЁОЬтФПЁПШчЭМЃЎвЛДЮКЏЪ§yЃН![]() x+1ЕФЭМЯѓL1НЛyжсгкЕуAЃЌвЛДЮКЏЪ§yЃНЉx+3ЕФЭМЯѓL2НЛxжсгкЕуBЃЌL1гыL2НЛгкЕуCЃЎ
x+1ЕФЭМЯѓL1НЛyжсгкЕуAЃЌвЛДЮКЏЪ§yЃНЉx+3ЕФЭМЯѓL2НЛxжсгкЕуBЃЌL1гыL2НЛгкЕуCЃЎ
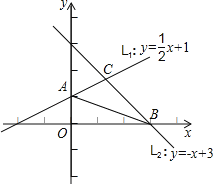
ЃЈ1ЃЉЧѓЕуAгыЕуBЕФзјБъЃЛ
ЃЈ2ЃЉЧѓЁїABCЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаетбљвЛИіЮЪЬтЃКЬНОПКЏЪ§![]() ЕФЭМЯѓгыаджЪЃЎ
ЕФЭМЯѓгыаджЪЃЎ
аЁЖЋИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдКЏЪ§![]() ЕФЭМЯѓгыаджЪНјааСЫЬНОПЃЎ
ЕФЭМЯѓгыаджЪНјааСЫЬНОПЃЎ
ЯТУцЪЧаЁЖЋЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъГЩЃК
ЃЈ1ЃЉЛЏМђКЏЪ§НтЮіЪНЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ___________ЃЌЕБ
___________ЃЌЕБ![]() ЪБ
ЪБ![]() ____________ЃЛ
____________ЃЛ
ЃЈ2ЃЉИљОнЃЈ1ЃЉжаЕФНсЙћЃЌЧыдкЫљИјзјБъЯЕжаЛГіКЏЪ§![]() ЕФЭМЯѓЃЛБИгУЭМ
ЕФЭМЯѓЃЛБИгУЭМ
ЃЈ3ЃЉНсКЯЛГіЕФКЏЪ§ЭМЯѓЃЌНтОіЮЪЬтЃКШєЙигк![]() ЕФЗНГЬ
ЕФЗНГЬ![]() жЛгавЛИіЪЕЪ§ИљЃЌжБНгаДГіЪЕЪ§
жЛгавЛИіЪЕЪ§ИљЃЌжБНгаДГіЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃК___________________________ЃЎ
ЕФШЁжЕЗЖЮЇЃК___________________________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкШчЭМЕФе§ЗНаЮЭјИёжаЃЌУПвЛИіаЁе§ЗНаЮЕФБпГЄЮЊ1ЃЌИёЕуШ§НЧаЮABCЃЈЖЅЕуЪЧЭјИёЯпНЛЕуЕФШ§НЧаЮ)ЕФЖЅЕуAЁЂCЕФзјБъЗжБ№ЪЧ(-5ЃЌ5)ЃЌ(-2ЃЌ3)ЃЎ

ЃЈ1ЃЉЧыдкЭМжаЕФЭјИёЦНУцФкЛГіЦНУцжБНЧзјБъЯЕxOyЃЛ
ЃЈ2ЃЉЧыЛГіЁїABCЙигкyжсЖдГЦЕФЁїA1B1C1ЃЌВЂаДГіЖЅЕуA1ЃЌB1ЃЌC1ЕФзјБъ
ЃЈ3ЃЉЧыдкxжсЩЯЧѓзївЛЕуPЃЌЪЙЁїPB1CЕФжмГЄзюаЁ.ЧыБъГіЕуPЕФЮЛжУЃЈБЃСєзїЭМКлМЃЃЌВЛашЫЕУїзїЭМЗНЗЈЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁбOЪЧЁїABCЕФЭтНгдВЃЌЁЯABC=45ЁуЃЌADЪЧЁбOЕФЧаЯпНЛBCЕФбгГЄЯпгкDЃЌABНЛOCгкEЃЎ
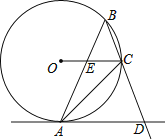
ЃЈ1ЃЉЧѓжЄЃКADЁЮOCЃЛ
ЃЈ2ЃЉШєAE=2![]() ЃЌCE=2ЃЎЧѓЁбOЕФАыОЖКЭЯпЖЮBEЕФГЄЃЎ
ЃЌCE=2ЃЎЧѓЁбOЕФАыОЖКЭЯпЖЮBEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com