
【题目】如图![]() ,抛物线
,抛物线![]() 与直线
与直线![]() 交于
交于![]() 、
、![]() 两点,过
两点,过![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .
.
![]() 求
求![]() 、
、![]() 、
、![]() 三点的坐标;
三点的坐标;
![]() 若点
若点![]() 是线段
是线段![]() 上的一个动点,过
上的一个动点,过![]() 作
作![]() 轴交抛物线于
轴交抛物线于![]() 点,连接
点,连接![]() 、
、![]() ,当
,当![]() 时,求
时,求![]() 的值;
的值;
![]() 如图
如图![]() ,连接
,连接![]() ,
,![]() 及
及![]() ,设点
,设点![]() 是
是![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 上任意一点,将
上任意一点,将![]() 沿边
沿边![]() 翻折得到
翻折得到![]() ,求当
,求当![]() 为何值时,
为何值时,![]() 与
与![]() 重叠部分的面积是
重叠部分的面积是![]() 面积的
面积的![]() .
.
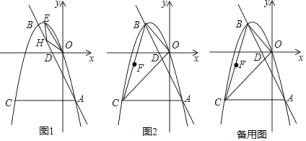
【答案】(1)点![]() 坐标
坐标![]() ,点
,点![]() 坐标
坐标![]() ,点
,点![]() 坐标
坐标![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 或
或![]() 时,
时,![]() 与
与![]() 重叠部分的面积是
重叠部分的面积是![]() 面积的
面积的![]() .
.
【解析】
(1)列方程组可知A、B两点坐标,根据点C的纵坐标与点A的纵坐标相同,列方程可求得点C坐标.
(2)如图1中,设![]() ,
,![]() ,则
,则![]() ,根据
,根据![]() 列出方程求出点H的横坐标,根据三角形的面积公式计算即可解决问题.
列出方程求出点H的横坐标,根据三角形的面积公式计算即可解决问题.
(3)分两种情形①若翻折后,点G在直线OC下方时,连接CG.如图2,可证四边形PFCG是平行四边形,得![]() ,在Rt△PBO中,根据
,在Rt△PBO中,根据![]() ,即可解决问题.②若翻折后,点G在直线OC上方时,连接CG.如图3,可证四边形PFGC是平行四边形,得
,即可解决问题.②若翻折后,点G在直线OC上方时,连接CG.如图3,可证四边形PFGC是平行四边形,得![]() 即可解决问题.
即可解决问题.
解:![]() 由
由![]() 解得
解得![]() 或
或![]() ,
,
∴点![]() 坐标
坐标![]() ,点
,点![]() 坐标
坐标![]() ,
,
∵![]() 轴,
轴,
∴点![]() 纵坐标为
纵坐标为![]() ,
,
由![]() ,解得
,解得![]() 或
或![]() ,
,
∴点![]() 坐标
坐标![]() .
.
![]() 如图
如图![]() 中,设
中,设![]() ,
,![]() ,则
,则![]() ,
,
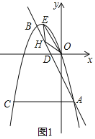
由题意![]() ,
,
解得![]() 或
或![]() (舍弃),
(舍弃),
∴![]() .
.
![]() ∵
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() .
.
①若翻折后,点![]() 在直线
在直线![]() 下方时,连接
下方时,连接![]() .如图
.如图![]() ,
,
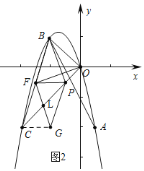
∵![]() ,
,
∴![]() ,
,
∴![]() .
.![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() .
.
②若翻折后,点![]() 在直线
在直线![]() 上方时,连接
上方时,连接![]() .如图
.如图![]() ,
,
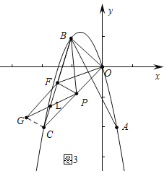
∵![]() ,
,
∴![]() ,
,
∴![]() .
.![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
综上所述:当![]() 或
或![]() 时,
时,![]() 与
与![]() 重叠部分的面积是
重叠部分的面积是![]() 面积的
面积的![]() .
.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
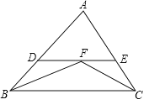
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,点点F作DE∥BC,交AB于点D,交AC于点E。若BD=3,DE=5,则线段EC的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快车和慢车都从甲地驶向乙地,两车同时出发行在同一条公路上,途中快车休息1小时后加速行驶比慢车提前0.5小时到达目的地,慢车没有体息整个行驶过程中保持匀速不变.设慢车行驶的时间为x小时,快车行驶的路程为y1千米,慢车行驶的路程为y2千米,图中折线OAEC表示y1与x之间的函数关系,线段OD表示y2与x之间的函数关系,请解答下列问题:
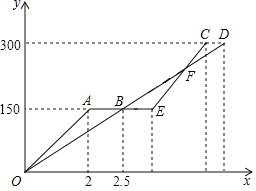
(1)甲、乙两地相距 千米,快车休息前的速度是 千米/时、慢车的速度是 千米/时;
(2)求图中线段EC所表示的y1与x之间的函数表达式;
(3)线段OD与线段EC相交于点F,直接写出点F的坐标,并解释点F的实际意义.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D是△ABC内一点,AD=BD,且AD⊥BD,连接CD.过点C作CE⊥BC交AD的延长线于点 E,连接BE.过点D作DF⊥CD交BC于点F.
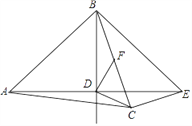
(1)若BD=DE=![]() ,CE=
,CE=![]() ,求BC的长;
,求BC的长;
(2)若BD=DE,求证:BF=CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.

(1)求证:AC平分∠DAO;
(2)若∠DAO=105°,∠E=30°.①求∠OCE的度数.②若⊙O的半径为![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“六一”儿童节前夕,某县教育局准备给留守儿童赠送一批学习用品,先对红星小学的留守儿童人数进行抽样统计,发现各班留守儿童人数分别为6名,7名,8名,10名,12名这五种情形,并绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
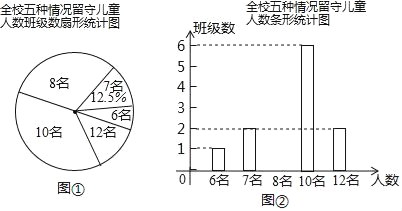
(1)该校有_____个班级,补全条形统计图;
(2)求该校各班留守儿童人数数据的平均数,众数与中位数;
(3)若该镇所有小学共有60个教学班,请根据样本数据,估计该镇小学生中,共有多少名留守儿童.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像分别与
的图像分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,以线段
,以线段![]() 为边在第四象限内作等腰直角
为边在第四象限内作等腰直角![]() ,且
,且![]() .
.
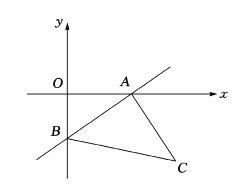
(1)试写出点![]() 的坐标:
的坐标: ![]() (_ _,_ ___),
(_ _,_ ___),![]() (_ ,_ )
(_ ,_ )
(2)求点![]() 的坐标;
的坐标;
(3)求直线![]() 的函数表达式
的函数表达式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,DE平分∠ADB,则∠B=( )
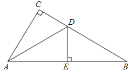
A. 40° B. 30° C. 25° D. 22.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com