
【题目】如图,已知抛物线的方程C1:![]() (m>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
(m>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧.
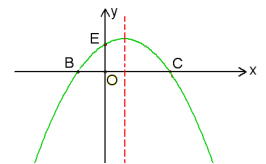
(1)若抛物线C1过点M(2, 2),求实数m的值;
(2)在(1)的条件下,在抛物线的对称轴上找一点H,使得BH+EH最小,求出点H的坐标;
(3)在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m的值;若不存在,请说明理由.
【答案】(1)4;(2)(1,![]() );(3)存在,m=
);(3)存在,m=![]() .
.
【解析】
试题分析:(1)将点(2,2)的坐标代入抛物线解析式,即可求得m的值;(2)根据轴对称以及两点之间线段最短的性质,可知点B、C关于对称轴x=1对称,连接EC与对称轴的交点即为所求的H点,如答图2所示;(3)本问需分两种情况进行讨论:①当△BEC∽△BCF时,如答图3所示.此时可求得m=2![]() +2;②当△BEC∽△FCB时,如答图4所示.此时可以得到矛盾的等式,故此种情形不存在.
+2;②当△BEC∽△FCB时,如答图4所示.此时可以得到矛盾的等式,故此种情形不存在.
试题解析:(1)将M(2,2)代入![]() ,得
,得![]() .解得m=4;
.解得m=4;
(2)如图2,抛物线的对称轴是直线x=1,当H落在线段EC上时,BH+EH最小,设对称轴与x轴的交点为P,那么![]() .因此
.因此![]() .解得
.解得![]() .所以点H的坐标为(1,
.所以点H的坐标为(1,![]() );
);
(3)①如图3,过点B作EC的平行线交抛物线于F,过点F作FF′⊥x轴于F′.由于∠BCE=∠FBC,所以当![]() ,即
,即![]() 时,△BCE∽△FBC.设点F的坐标为
时,△BCE∽△FBC.设点F的坐标为![]() ,由
,由![]() ,得
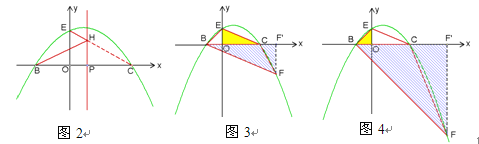
,得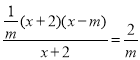 .解得x=m+2.所以F′(m+2, 0).由
.解得x=m+2.所以F′(m+2, 0).由![]() ,得
,得![]() .所以
.所以![]() .由
.由![]() ,得
,得![]() .整理,得0=16.此方程无解.
.整理,得0=16.此方程无解.
②如图4,作∠CBF=45°交抛物线于F,过点F作FF′⊥x轴于F′,由于∠EBC=∠CBF,所以![]() ,即
,即![]() 时,△BCE∽△BFC.在Rt△BFF′中,由FF′=BF′,得
时,△BCE∽△BFC.在Rt△BFF′中,由FF′=BF′,得![]() .解得x=2m.所以F′
.解得x=2m.所以F′![]() .所以BF′=2m+2,
.所以BF′=2m+2,![]() .由
.由![]() ,得
,得![]() .解得
.解得![]() .综合①、②,符合题意的m=
.综合①、②,符合题意的m=![]() .
.


科目:初中数学 来源: 题型:
【题目】由于受到手机更新换代的影响,某手机店经销的甲品牌手机四月份售价比三月份每台降价500元.如果卖出相同数量的甲品牌手机,那么三月份销售额为9万元,四月份销售额只有8万元.
(1)四月份甲品牌手机每台售价为多少元?
(2)为了提高利润,该店计划五月份购进甲品牌及乙品牌手机销售,已知甲每台进价为3500元,乙每台进价为4000元,预算用不多于7.6万元且不少于7.5万元的资金购进这两种手机共20台,问按此预算要求,可以有几种进货方案,请写出所有进货方案?
(3)该店计划五月在销售甲品牌手机时,在四月份售价基础上每售出一台甲品牌手机再返还顾客现金![]() 元,而乙品牌手机按销售价4400元销售,如要使(2)中所有方案获利相同,
元,而乙品牌手机按销售价4400元销售,如要使(2)中所有方案获利相同,![]() 应取何值?
应取何值?
查看答案和解析>>
科目:初中数学 来源: 题型:
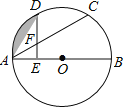
【题目】如图,C、D是半圆O上的三等分点,直径AB=4,连接AD、AC,DE⊥AB,垂足为E,DE交AC于点F.
(1)求∠AFE的度数;
(3)求阴影部分的面积(结果保留π和根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
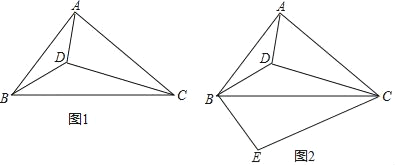
【题目】如图1,设D为锐角△ABC内一点,∠ADB=∠ACB+90°.
(1)求证:∠CAD+∠CBD=90°;
(2)如图2,过点B作BE⊥BD,BE=BD,连接EC,若ACBD=ADBC,
①求证:△ACD∽△BCE;
②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx过点B(1,﹣3),对称轴是直线x=2,且抛物线与x轴的正半轴交于点A.
(1)求抛物线的解析式,并根据图象直接写出当y≤0时,自变量x的取值范图;
(2)在第二象限内的抛物线上有一点P,当PA⊥BA时,求△PAB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
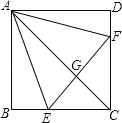
【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有____.(填序号即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菜农李伟种植的某蔬菜计划以每千克![]() 元的单价对外批发销售,由于部分菜农盲目扩大种植,造成该蔬菜滞销.李伟为了加快销售,减少损失,对价格经过两次下调后,以每千克
元的单价对外批发销售,由于部分菜农盲目扩大种植,造成该蔬菜滞销.李伟为了加快销售,减少损失,对价格经过两次下调后,以每千克![]() 元的单价对外批发销售.
元的单价对外批发销售.
![]() 求平均每次下调的百分率;
求平均每次下调的百分率;
![]() 小华准备到李伟处购买
小华准备到李伟处购买![]() 吨该蔬菜,因数量多,李伟决定再给予两种优惠方案以供选择:
吨该蔬菜,因数量多,李伟决定再给予两种优惠方案以供选择:
方案一:打九折销售;
方案二:不打折,每吨优惠现金![]() 元.
元.
试问小华选择哪种方案更优惠,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度,根据所给的直角坐标系(O是坐标原点),解答下列问题:
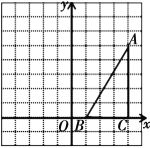
(1)画出平移后的△A′B′C′,并直接写出点A′、B′、C′的坐标;
(2)求在平移过程中线段AB扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB、连接DO并延长交CB的延长线于点E.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若BE=4,DE=8,求AC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com