
【题目】如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°.
(1)求证:BD=AE;
(2)若△ACB不动,把△DCE绕点C旋转到使点D落在AB边上,如图2所示,问上述结论还成立吗?若成立,给予证明.

 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.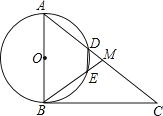
(1)求证:MD=ME;
(2)填空:
①若AB=6,当AD=2DM时,DE=;
②连接OD,OE,当∠A的度数为时,四边形ODME是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是轴对称图形,且直线AC是对称轴,AB∥CD,则下列结论:①AC⊥BD;②AD∥BC;③四边形ABCD是菱形;④△ABD≌△CDB.其中正确的是(只填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=12,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F,则△ACF与△BDF的周长之和为 ___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在4×4正方形网格中,有3个小正方形已经涂黑,若再涂黑任意一个白色的小正方形(每一个白色的小正方形被涂黑的可能性相同),使新构成的黑色部分的图形是轴对称图形的概率是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4)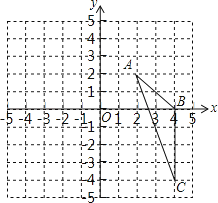
(1)请画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的 ![]() ,得到△A2B2C2 , 请在y轴右侧画出△A2B2C2 , 并求出∠A2C2B2的正弦值.
,得到△A2B2C2 , 请在y轴右侧画出△A2B2C2 , 并求出∠A2C2B2的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC=90°,AB=DB,EB=CB,M,N分别是AE,CD的中点.
(1)求证:△ABM≌△DBN;
(2)试探索BM和BN的关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCO是平行四边形,OA=2,AB=6,点C在x轴的负半轴上,将ABCO绕点A逆时针旋转得到ADEF,AD经过点O,点F恰好落在x轴的正半轴上,若点D在反比例函数y= ![]() (x<0)的图象上,则k的值为
(x<0)的图象上,则k的值为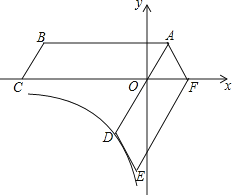
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com