
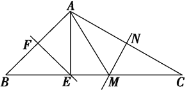
【题目】如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC=90°,AB=DB,EB=CB,M,N分别是AE,CD的中点.
(1)求证:△ABM≌△DBN;
(2)试探索BM和BN的关系,并证明你的结论.

【答案】(1)见解析;(2)△MBN是等腰直角三角形,理由见解析
【解析】
(1)根据SAS即可证明结论;(2)通过证明△ABM≌△DBN可证明BM=BN,∠ABM=∠DBN.根据∠ABD=∠DBC,∠ABD+∠DBC=180°可得∠DBN+∠DBM=∠MBN=90°,即可得答案.
(1)解:在△ABE和△DBC中 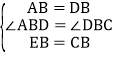 ,
,
∴△ABE≌△DBC
(2)解:△MBN是等腰直角三角形,证明如下:
∵△ABE≌△DBC,
∴AE=CD,∠BAM=∠BDN.
∵M,N分别是AE,CD的中点,
∴AM=![]() AE,CN=
AE,CN=![]() CD.
CD.
∴AM=CN.
在△ABM和△DBN中 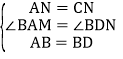 ,
,
∴ABM≌△DBN.
∴BM=BN,∠ABM=∠DBN.
∵∠ABD=∠DBC,∠ABD+∠DBC=180°,
∴∠ABD=∠ABM+∠DBM=90°.
∴∠DBN+∠DBM=∠MBN=90°.
∴△MBN是等腰直角三角形.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】如图,用(-1,0)表示A点的位置,用(2,1)表示B点的位置,那么:

(1)画出直角坐标系。
(2)写出△DEF的三个顶点的坐标。
(3)在图中表示出点M(6,2),N(4,4)的位置。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°.
(1)求证:BD=AE;
(2)若△ACB不动,把△DCE绕点C旋转到使点D落在AB边上,如图2所示,问上述结论还成立吗?若成立,给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在南宁市地铁1号线某段工程建设中,甲队单独完成这项工程需要150天,甲队单独施工30天后增加乙队,两队又共同工作了15天,共完成总工程的 ![]() .
.
(1)求乙队单独完成这项工程需要多少天?
(2)为了加快工程进度,甲、乙两队各自提高工作效率,提高后乙队的工作效率是 ![]() ,甲队的工作效率是乙队的m倍(1≤m≤2),若两队合作40天完成剩余的工程,请写出a关于m的函数关系式,并求出乙队的最大工作效率是原来的几倍?
,甲队的工作效率是乙队的m倍(1≤m≤2),若两队合作40天完成剩余的工程,请写出a关于m的函数关系式,并求出乙队的最大工作效率是原来的几倍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下面是利用尺规作∠AOB的角平分线OC的作法:
①以点O为圆心,任意长为半径作弧,交OA、OB于点D,E;
②分别以点D,E为圆心,以大于![]() DE的长为半径作弧,两弧在∠AOB内部交于点C;
DE的长为半径作弧,两弧在∠AOB内部交于点C;
③作射线OC,则射线OC就是∠AOB的平分线.
以上用尺规作角平分线时,用到的三角形全等的判定方法是( )

A. SSS B. SAS
C. ASA D. AAS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是某市一座人行天桥的示意图,天桥离地面的高BC是10米,坡面10米处有一建筑物HQ,为了方便使行人推车过天桥,市政府部门决定降低坡度,使新坡面DC的倾斜角∠BDC=30°,若新坡面下D处与建筑物之间需留下至少3米宽的人行道,问该建筑物是否需要拆除(计算最后结果保留一位小数).(参考数据: ![]() =1.414,
=1.414, ![]() =1.732)
=1.732)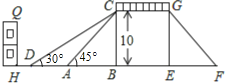
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形的边OA在x轴上,边OC在y轴上,点B的坐标为(10,8),沿直线OD折叠矩形,使点A正好落在BC上的E处,E点坐标为(6,8),抛物线y=ax2+bx+c经过O、A、E三点.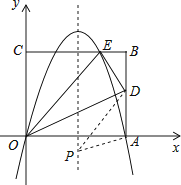
(1)求此抛物线的解析式;
(2)求AD的长;
(3)点P是抛物线对称轴上的一动点,当△PAD的周长最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的垂直平分线,E、M在BC上,则∠EAM等于 ( )
A. 58° B. 32°
C. 36° D. 34°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com