练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，在△ABC中，∠BAC=106°，EF、MN分别是AB、AC的垂直平分线，E、M在BC上，则∠EAM等于 ( )

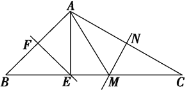
    A. 58° B. 32°

    C. 36° D. 34°

    【答案】B

    【解析】

    先由∠BAC=106°及三角形内角和定理求出∠B+∠C的度数，再根据线段垂直平分线的性质求出∠B=∠BAE，∠C=∠CAN，即∠B+∠C=∠BAE+∠CAN，由∠EAN=∠BAC-（∠BAE+∠CAN）解答即可．

    ∵△ABC中,∠BAC=106°，

    ∴∠B+∠C=180°∠BAC=180°106°=74°，

    ∵EF、MN分别是AB、AC的中垂线，

    ∴∠B=∠BAE，∠C=∠CAN，

    即∠B+∠C=∠BAE+∠CAN=74°，

    ∴∠EAN=∠BAC(∠BAE+∠CAN)=106°74°=32°.

    故答案为B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD是轴对称图形，且直线AC是对称轴，AB∥CD，则下列结论：①AC⊥BD；②AD∥BC；③四边形ABCD是菱形；④△ABD≌△CDB．其中正确的是（只填写序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点B在线段AC上，点E在线段BD上，∠ABD＝∠DBC＝90°，AB＝DB，EB＝CB，M，N分别是AE，CD的中点．

    （1）求证：△ABM≌△DBN；

    （2）试探索BM和BN的关系，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数学课上，老师出示了如下的题目：如图（1），在等边△ABC中，点E在AB上，点D在CB的延长线上，且ED=EC，试判断AE和BD的大小关系，并说明理由．

    小敏与同桌小聪讨论后，进行了如下解答：

    （1）特殊情况，探索结论

    当点E为AB的中点时，如图（2），确定线段AE与DB的大小关系，请你直接写出结论：AE DB（填“>”，“<”或“=”）；

    （2）特例启发，解答题目

    如图（1），试判断AE和BD的大小关系，并说明理由；

    （3）拓展结论，设计新题

    在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED=EC；若△ABC的边长为1，AE=2，请画出图形，求CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠C=90°，AC=3，BC=4，点O是BC中点，将△ABC绕点O旋转得△A′B' C′，则在旋转过程中点A、C′两点间的最大距离是_______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点B，F，C，E在直线l上（F，C之间不能直接测量），点A，D在l异侧，测得AB=DE，AC=DF，BF=EC.

    （1）求证：△ABC≌△DEF；

    （2）指出图中所有平行的线段，并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCO是平行四边形，OA=2，AB=6，点C在x轴的负半轴上，将ABCO绕点A逆时针旋转得到ADEF，AD经过点O，点F恰好落在x轴的正半轴上，若点D在反比例函数y= （x＜0）的图象上，则k的值为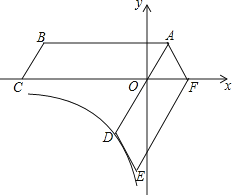

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个y关于x的函数同时满足两个条件：①图象过（2，1）点；②当x＞0时，y随x的增大而减小．这个函数解析式为 ． （写出一个即可）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，A、C、F、D在同一直线上，AF＝DC，AB∥DE，AB＝DE.

    求证：(1) △ABC≌△DEF；

    (2)BC∥EF.

    查看答案和解析>>

    同步练习册答案