
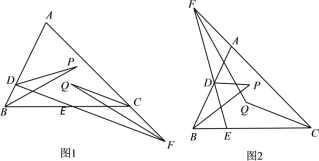
【题目】已知D、E分别为△ABC中AB、BC上的动点,直线DE与直线AC相交于F,∠ADE的平分线与∠B的平分线相交于P,∠ACB的平分线与∠F的平分线相交于Q.
(1)如图1,当F在AC的延长线上时,求∠P与∠Q之间的数量关系;
(2)如图2,当F在AC的反向延长线上时,求∠P与∠Q之间的数量关系(用等式表示).
【答案】(1)∠P=∠Q;(2)∠P+∠Q=180°.
【解析】
(1)先根据三角形内角和定理和三角形外角的性质求出2∠P=∠DEB,2∠Q=∠CEF,即可得出答案;
(2)先根据三角形内角和定理和三角形外角的性质求出∠P=![]() ∠BED,∠Q=90°+
∠BED,∠Q=90°+![]() ∠FEC,根据邻补角互补求出即可.
∠FEC,根据邻补角互补求出即可.
解:(1)∵DP是∠ADF的平分线,BP是∠ABC的平分线,
∴∠ADF=2∠ADP,∠ABC=2∠ABP,
∵∠ADF=∠ABC+∠DEB,∠ADP=∠P+∠ABP,
∴2∠ADP=2∠P+2∠ABP,
∴∠DEB=2∠P,
同理∠CEF=2∠Q,
∵∠DEB=∠CEF,
∴2∠P=2∠Q,
∴∠P=∠Q;
(2)∠P+∠Q=180°,
理由是:∵由(1)知:2∠P=∠BED,
∴∠P=![]() ∠BED,
∠BED,
∵FQ是∠CFE的平分线,CQ是∠ACB的平分线,
∴∠QFC=![]() ∠EFC,∠QCF=
∠EFC,∠QCF=![]() ∠ACB,
∠ACB,
∵∠FEC+∠EFC+∠ECF=180°,
∴∠EFC+∠ECF=180°-∠FEC,
∴∠Q=180°-(∠QFC+∠QCF)
=180°-![]() (∠EFC+∠ECF)
(∠EFC+∠ECF)
=180°-![]() (180°-∠FEC)
(180°-∠FEC)
=90°+![]() ∠FEC,
∠FEC,
∴∠P+∠Q=![]() ∠BED+90°+
∠BED+90°+![]() ∠FEC
∠FEC
=90°+![]() (∠BED+∠FEC)
(∠BED+∠FEC)
=90°+![]() ×180°
×180°
=180°.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图所示,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B'点,AE是折痕。

(1)试判断B'E与DC的位置关系并说明理由。
(2)如果∠C=130°,求∠AEB的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在函数y=﹣ ![]() (x<0)的图象上,点B在函数y=
(x<0)的图象上,点B在函数y= ![]() (x>0)的图象上,点C在x轴上.若四边形OABC为平行四边形,则△OBC的面积为 .
(x>0)的图象上,点C在x轴上.若四边形OABC为平行四边形,则△OBC的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点0是等边△ABC内一点,∠AOB=110°,∠BOC=α,OC=CD,
且∠DOC=60°连接OD.
(1)求证:△COD是等边三角形
(2)当α=150°时,试判断△AOD的形状,并说明理由
(3)探究:当α为多少度时,△AOD是等腰三角形

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:
①AD∥BC;②∠BDC=![]() ∠BAC;③∠ADC=90°-∠ABD; ④BD平分∠ADC.
∠BAC;③∠ADC=90°-∠ABD; ④BD平分∠ADC.
其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若点B,P在直线a的异侧,BM⊥直线a于点M.CN⊥直线a于点N,连接PM,PN. 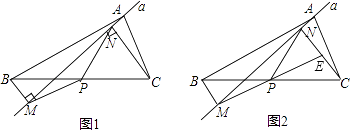
(1)延长MP交CN于点E(如图2). 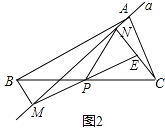
①求证:△BPM≌△CPE;
②求证:PM=PN;
(2)若直线a绕点A旋转到图3的位置时,点B,P在直线a的同侧,其它条件不变,此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由; 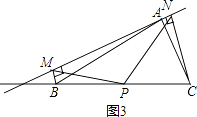
(3)若直线a绕点A旋转到与BC边平行的位置时,其它条件不变,请直接判断四边形MBCN的形状及此时PM=PN还成立吗?不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形,并将添加的全等条件标注在图上.
请你参考这个作全等三角形的方法,解答下列问题:
(1)如图2,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC和∠BCA的平分线,AD、CE相交于点F,求∠EFA的度数;
(2)在(1)的条件下,请判断FE与FD之间的数量关系,并说明理由;
(3)如图3,在△ABC中,如果∠ACB不是直角,而( 1 )中的其他条件不变,试问在(2)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学有一块四边形的空地ABCD,如图所示,为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com