
【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:
①AD∥BC;②∠BDC=![]() ∠BAC;③∠ADC=90°-∠ABD; ④BD平分∠ADC.
∠BAC;③∠ADC=90°-∠ABD; ④BD平分∠ADC.
其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
根据角平分线定义得出∠ABC=2∠ABD=2∠DBC,∠EAC=2∠EAD,∠ACF=2∠DCF,根据三角形的内角和定理得出∠BAC+∠ABC+∠ACB=180°,根据三角形外角性质得出∠ACF=∠ABC+∠BAC,∠EAC=∠ABC+∠ACB,根据已知结论逐步推理,即可判断各项.
解:∵AD平分∠EAC,
∴∠EAC=2∠EAD,
∵∠EAC=∠ABC+∠ACB,∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,
∴①正确;
∵∠ACF=2∠DCF,∠ACF=∠BAC+∠ABC,∠ABC=2∠DBC,∠DCF=∠DBC+∠BDC,
∴∠BAC=2∠BDC,
∠BDC=![]() ∠BAC,
∠BAC,
∴②正确;
在△ADC中,∠ADC+∠CAD+∠ACD=180°,
∵CD平分△ABC的外角∠ACF,
∴∠ACD=∠DCF,
∵AD∥BC,
∴∠ADC=∠DCF,∠ADB=∠DBC,∠CAD=∠ACB
∴∠ACD=∠ADC,∠CAD=∠ACB=∠ABC=2∠ABD,
∴∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,
∴∠ADC+∠ABD=90°
∴∠ADC=90°-∠ABD,
故③正确;
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵∠ADB=∠DBC,∠ADC=90°-![]() ∠ABC,
∠ABC,
∴∠ADB不等于∠CDB,
∴④不正确;
即正确的有3个,
故选C.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABFG和正方形CDEF的顶点在边长为1的正方形网格的格点上.
(1)建立平面直角坐标系,使点B,C的坐标分别为(0,0)和(5,0),并写出点A,D,E,F,G的坐标;
(2)连接BE和CG相交于点H,BE和CG相等吗?并计算∠BHC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连接AB、AE、BE.已知tan∠CBE= ![]() ,A(3,0),D(﹣1,0),E(0,3).
,A(3,0),D(﹣1,0),E(0,3).
(1)求抛物线的解析式及顶点B的坐标;
(2)求证:CB是△ABE外接圆的切线;
(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,直接写出点P的坐标;若不存在,请说明理由;
(4)设△AOE沿x轴正方向平移t个单位长度(0<t≤3)时,△AOE与△ABE重叠部分的面积为s,求s与t之间的函数关系式,并指出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=BC,D为边AB中点,点E、F分别在射线CA、BC上,且AE=CF,连结EF.
猜想:如图①,当点E、F分别在边CA和BC上时,线段DE与DF的大小关系为________.
探究:如图②,当点E、F分别在边CA、BC的延长线上时,判断线段DE与DF的大小关系,并加以证明.
应用:如图②,若DE=4,利用探究得到的结论,求△DEF的面积.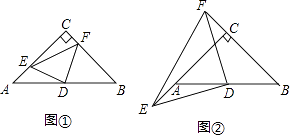
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=4,点P从点C出发沿CA以每秒1个单位长度的速度向终点A运动:同时,点Q从点C出发沿CB﹣BA运动,点Q在CB上的速度为每秒2个单位长度,在BA上的速度为每秒 ![]() 个单位长度,当点P到达终点A时,点Q随之停止运动.以CP、CQ为邻边作CPMQ,设CPMQ与△ABC重叠部分图形的面积为y(平方单位),点P的运动时间为x(秒).
个单位长度,当点P到达终点A时,点Q随之停止运动.以CP、CQ为邻边作CPMQ,设CPMQ与△ABC重叠部分图形的面积为y(平方单位),点P的运动时间为x(秒).
(1)当点M落在AB上时,求x的值.
(2)当点Q在边CB上运动时,求y与x的函数关系式.
(3)在P、Q两点整个运动过程中,当CPMQ与△ABC重叠部分图形不是四边形时,求x的取值范围.
(4)以B、C、M为顶点的三角形是等腰三角形时,直接写出CP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知D、E分别为△ABC中AB、BC上的动点,直线DE与直线AC相交于F,∠ADE的平分线与∠B的平分线相交于P,∠ACB的平分线与∠F的平分线相交于Q.
(1)如图1,当F在AC的延长线上时,求∠P与∠Q之间的数量关系;
(2)如图2,当F在AC的反向延长线上时,求∠P与∠Q之间的数量关系(用等式表示).
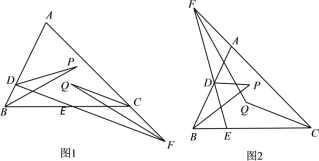
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【背景】国家为扶持软件企业的发展,对企业实行月补贴,以提高企业的净利润.
【问题】国内某软件企业2014 年12月份并未如期收到700万元的月补贴,这样导致2014 年的净利润增长只有55%.而若补贴及时到位,则2014 年的净利润增长将达到60%.
(1)求2013年该企业净利润是多少万元?
(2)又据统计,2014年12月该企业不含月补贴的月净利润为2100万元,2015年1月及2月不含月补贴的月净利润比上月增加的百分数分别是m和 2m,这两个月的月补贴相等,且都在2014年12月基础上增加了2m.据推算,若以后各月不含月补贴的月净利润和月补贴均稳定在2月份的水平不变,则 2015年该企业净利润将达到2013年的3倍,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为3,F为BC边上的动点,FD⊥AB于D,FE⊥AC于E,则DE的长为( )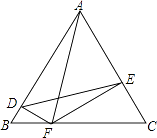
A.随F点运动,其值不变
B.随F点运动而变化,最大值为 ![]()
C.随F点运动而变化,最小值为 ![]()
D.随F点运动而变化,最小值为 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com