
【题目】在Rt△ABC中,∠ACB=90°,AC=BC,D为边AB中点,点E、F分别在射线CA、BC上,且AE=CF,连结EF.
猜想:如图①,当点E、F分别在边CA和BC上时,线段DE与DF的大小关系为________.
探究:如图②,当点E、F分别在边CA、BC的延长线上时,判断线段DE与DF的大小关系,并加以证明.
应用:如图②,若DE=4,利用探究得到的结论,求△DEF的面积.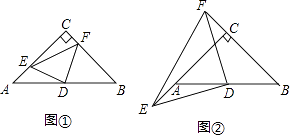
【答案】猜想:DE=DF.
如图1,连结CD,
∵∠ACB=90°,AC=BC,
∴∠CAD=45°,
∵D为边AB的中点,
∴CD=AD,∠BCD= ![]() ∠ACB=45°,
∠ACB=45°,
∴∠EAD=∠FCD,
在△AED和△CFD中
∴△ADE≌△CFD(SAS),
∴DE=DF,
故答案为:DE=DF;
探究:DE=DF,证明如下:
如图2,连接CD,
∵∠ACB=90°,AC=BC,
∴∠CAD=45°,
∵D为AB中点,
∴AD=CD,∠BCD= ![]() ∠ACB=45°,
∠ACB=45°,
∵∠CAD+∠EAD=∠BCD+∠FCD=180°,
∴∠EAD=∠FCD=135°,
在△ADE和△CDF中
∴△ADE≌△CDF(SAS),
∴DE=DF;
应用:
∵△ADE≌△CDF,
∴∠ADE=∠CDF,
∵∠ADC=90°,
∴∠EDF=90°,
∵DE=DF=4,
∴S△DEF= ![]() DE2=
DE2= ![]() ×42=8.
×42=8.
【解析】猜想:连接CD,可证明△ADE≌△CFD,可得出结论;探究:连接CD,同(1)可证明△ADE≌△CFD,可证得DE=DF;应用:由△ADE≌△CFD可证得∠EDF=90°,容易求得△DEF的面积.
【考点精析】本题主要考查了全等三角形的性质的相关知识点,需要掌握全等三角形的对应边相等; 全等三角形的对应角相等才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣kx+k﹣1=0.
(1)求证:此一元二次方程恒有实数根.
(2)无论k为何值,该方程有一根为定值,请求出此方程的定值根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个可以自由转动的转盘被平均分成3个扇形,分别标有1、2、3三个数字,小王和小李各转动一次转盘为一次游戏,当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转). 
(1)请你用树状图或列表的方法表示出每次游戏可能出现的所有结果;
(2)两次转盘,第一次转得的数字记为m,第二次记为n,A的坐标为(m,n),则A点在函数y= ![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在函数y=﹣ ![]() (x<0)的图象上,点B在函数y=
(x<0)的图象上,点B在函数y= ![]() (x>0)的图象上,点C在x轴上.若四边形OABC为平行四边形,则△OBC的面积为 .
(x>0)的图象上,点C在x轴上.若四边形OABC为平行四边形,则△OBC的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,D、E分别为边AB、BC的中点,点F在边AC的延长线上,∠FEC=∠B,求证:四边形CDEF是平行四边形.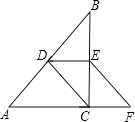
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点0是等边△ABC内一点,∠AOB=110°,∠BOC=α,OC=CD,
且∠DOC=60°连接OD.
(1)求证:△COD是等边三角形
(2)当α=150°时,试判断△AOD的形状,并说明理由
(3)探究:当α为多少度时,△AOD是等腰三角形

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:
①AD∥BC;②∠BDC=![]() ∠BAC;③∠ADC=90°-∠ABD; ④BD平分∠ADC.
∠BAC;③∠ADC=90°-∠ABD; ④BD平分∠ADC.
其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若点B,P在直线a的异侧,BM⊥直线a于点M.CN⊥直线a于点N,连接PM,PN. 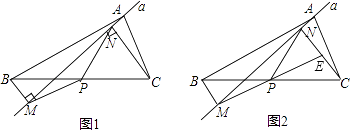
(1)延长MP交CN于点E(如图2). 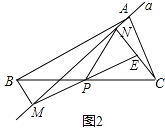
①求证:△BPM≌△CPE;
②求证:PM=PN;
(2)若直线a绕点A旋转到图3的位置时,点B,P在直线a的同侧,其它条件不变,此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由; 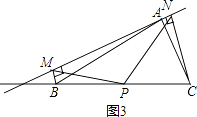
(3)若直线a绕点A旋转到与BC边平行的位置时,其它条件不变,请直接判断四边形MBCN的形状及此时PM=PN还成立吗?不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,半径OA垂直于弦BC,垂足为E,点D在CA的延长线上,若∠DAB+
∠AOB=60°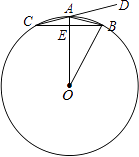
(1)求∠AOB的度数;
(2)若AE=1,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com