
【题目】已知关于x的一元二次方程x2﹣kx+k﹣1=0.
(1)求证:此一元二次方程恒有实数根.
(2)无论k为何值,该方程有一根为定值,请求出此方程的定值根.
【答案】
(1)证明:∵△=b2﹣4ac=(﹣k)2﹣4×1×(k﹣1)=k2﹣4k+4=(k﹣2)2≥0,
∴此一元二次方程恒有实数根.
(2)解:解方程x2﹣kx+k﹣1=0,得
![]() ,
,
解得x1=k﹣1,x2=1.
其中根X=1与k的取值无关,所以此方程的定值根为x=1.
【解析】(1)由根的判别式的符号来判定关于x的一元二次方程x2﹣kx+k﹣1=0的根的情况.(2)利用求根根式求得方程的两个根,得到其中一根是常数.
【考点精析】关于本题考查的求根公式,需要了解根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根才能得出正确答案.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,点D在AC上,点E在BC的延长线上,且BD=DE. 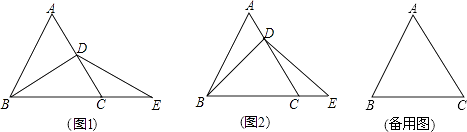
(1)若点D是AC的中点,如图1,求证:AD=CE.
(2)若点D不是AC的中点,如图2,试判断AD与CE的数量关系,并证明你的结论:(提示:过点D作DF∥BC,交AB于点F.)
(3)若点D在线段AC的延长线上,(2)中的结论是否仍成立?如果成立,给予证明;如果不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以BC为直径的圆交△ABC的两边AB、AC于点D、E,点E恰为AC的中点,BF为△ABC的外角平分线,点F在圆上,请你仅用一把无刻度的直尺,过点A作一条线段,将△ABC分成面积相等的两部分. 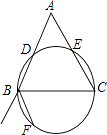
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司市场营销部的营销员的个人月收入y(元)与该营销员每月的销售量x(万件)成一次函数关系,其图象如图11所示.根据图象提供的信息,解答下列问题:
(1)求出营销员的个人月收入y(元)与该营销员每月的销售量x(万件)(x≥0)之间的函数关系式;
(2)已知该公司营销员李平5月份的销售量为1.2万件,求李平5月份的收入.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正△ABC与等腰△ADE的顶点A重合,AD=AE,∠DAE=30°,将△ADE绕顶点A旋转,在旋转过程中,当BD=CE时,∠BAD的大小可以是 . 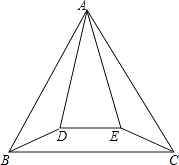
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中有A(-2,1),B(3,1),C(2,3)三点.请回答下列问题:
(1)在坐标系内描出点A,B,C的位置.
(2)求出以A,B,C三点为顶点的三角形的面积.
(3)在y轴上是否存在点P,使以A,B,P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABFG和正方形CDEF的顶点在边长为1的正方形网格的格点上.
(1)建立平面直角坐标系,使点B,C的坐标分别为(0,0)和(5,0),并写出点A,D,E,F,G的坐标;
(2)连接BE和CG相交于点H,BE和CG相等吗?并计算∠BHC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=BC,D为边AB中点,点E、F分别在射线CA、BC上,且AE=CF,连结EF.
猜想:如图①,当点E、F分别在边CA和BC上时,线段DE与DF的大小关系为________.
探究:如图②,当点E、F分别在边CA、BC的延长线上时,判断线段DE与DF的大小关系,并加以证明.
应用:如图②,若DE=4,利用探究得到的结论,求△DEF的面积.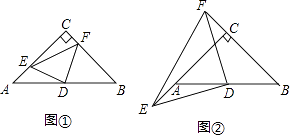
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com